Théorèmes de géométrie dans les triangles
Plan de cours
Concentré du cours de géométrie du collège, contenant :
- les relations entre le triangle rectangle et le cercle ;
- les propriétés de Pythagore ;
- les propriétés des milieux ;
- les propriétés de Thalès.
Sans démonstration.
1- Propriété des angles
Théorème 1
Dans un triangle, la somme des trois angles vaut 180°.
Précisément, pour un triangle , on a la relation
Cette relation permet de calculer la mesure en degrés d’un angle dès que l’on connaît celles des deux autres.
2 - Propriétés du cercle circonscrit
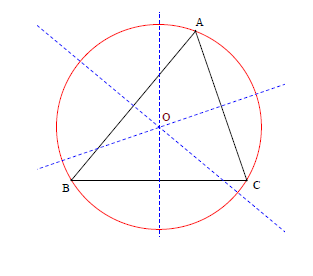
Il est bien connu que, pour tout triangle , il existe un unique cercle passant par les trois sommets , et : c’est le cercle circonscrit au triangle.
Son centre est situé à l’intersection des médiatrices de chacun des côtés du triangle : ce point est équidistant des sommets.
2.1 - Le théorème direct
On rappelle que, dans un triangle rectangle, le côté qui est opposé à l’angle droit est appelé hypoténuse.
Théorème 2
Pour tout triangle rectangle, le milieu de l’hypoténuse est le
centre du cercle circonscrit.
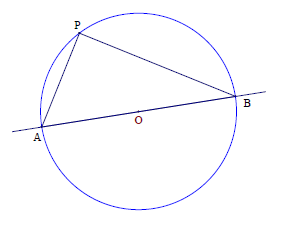
Lorsque l’angle est droit, alors est un diamètre du cercle circonscrit au triangle .
En conséquence, la médiane issue de l’angle droit est un rayon du cercle, et donc mesure la moitié de l’hypoténuse :
Ce théorème permet de prouver que le sommet de l’angle droit est situé sur un cercle particulier ; il permet aussi de calculer la longueur de la médiane issue de l’angle droit.
2.2 La réciproque
Théorème 3
Le triangle formé en reliant un point situé sur un cercle aux
extrémités de l’un de ses diamètres est un triangle rectangle.
Précisément, si est un diamètre du cercle et si est un point de ce cercle, alors le triangle est rectangle en .
C’est un théorème permettant de prouver qu’un triangle est rectangle.
3 Propriétés de Pythagore
3.1 Le théorème direct
Théorème 4
Dans un triangle rectangle, le carré de l’hypoténuse est égal
à la somme des carrés des côtés de l’angle droit.
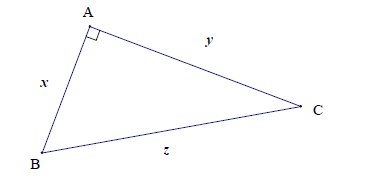
Dans la figure suivante, en notant , et , on a :
C’est la relation de Pythagore entre les côtés , et d’un triangle rectangle.
Lorsqu’un triangle est rectangle, on peut donc calculer l’un des côtés à partir des deux autres.
On peut aussi utiliser ainsi ce théorème : si l’on connaît les trois côtés et si ceux-ci ne vérifient pas la relation de Pythagore, alors le triangle n’est pas rectangle.
3.2 La réciproque
Théorème 5
Dans un triangle, si le carré du plus grand des côtés est égal à la somme des carrés des deux plus petits côtés, alors le triangle est rectangle.
Lorsqu’on connaît les longueurs des trois côtés , et , on peut donc prouver qu’un triangle est rectangle si ces nombres vérifient la relation de Pythagore.
4 Propriétés des milieux
4.1 Le théorème direct
Théorème 6
_Dans tout triangle, les milieux de deux côtés sont tels que
- la droite qui joint ces milieux est parallèle au troisième côté,
- le segment qui joint ces milieux mesure la moitié du troisième côté.
Ci-dessous, étant le milieu de et étant celui de , alors on a :
et .
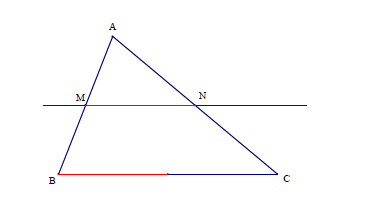
Ce théorème permet dans certains cas de prouver que deux droites sont parallèles ou bien de calculer une longueur.
4.2 La réciproque
Théorème 7
Dans un triangle, si une droite passe par le milieu d’un côté
en étant parallèle à un deuxième côté, alors elle coupe nécessairement le troisième côté en son milieu.
Ceci permet de prouver qu’un point donné est le milieu d’un segment.
5 Propriétés de Thalès
5.1 Le théorème direct
Théorème 8
Deux triangles à côtés parallèles ont leurs côtés proportionnels ; précisément si et sont sécantes en , et si est parallèle à , alors on a :
Ci-dessous, on illustre les deux cas de figure habituels, selon que les parallèles sont d’un même côté du sommet (configuration « triangulaire ») ou bien sont situées de part et d’autre de (configuration « papillon »).
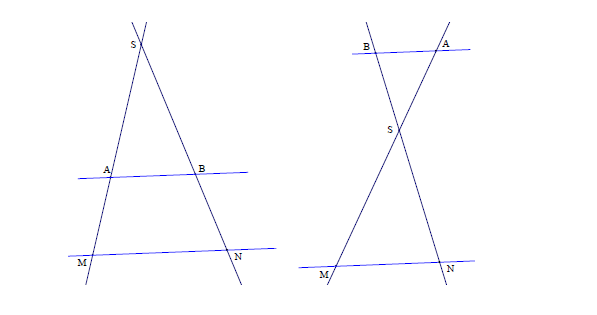
Ce théorème permet de calculer un côté à partir d’autres, sachant le parallélisme des côtés. Il permet aussi de prouver que des droites ne sont pas parallèles (lorsque les rapports ne sont pas égaux).
5.2 La réciproque
Théorème 9
Lorsque et sont sécantes en et si :
- d’une part, les points , et se suivent dans le même ordre que les points , et ,
- d’autre part, les rapports et sont égaux,
alors les droites et sont parallèles.
C’est un théorème permettant de prouver que deux droites sont parallèles dans des conditions strictes d’alignement et de proportionnalité.
Plus d'informations
Ce cours sur les théorèmes dans les triangles peut être complété par des outils pratiques. Ces outils vous permettent de calculer (et de vérifier vos calculs parfois) le périmètre ou l'aire d'un triangle par exemple (quelle que soit sa propriété : rectangle, isocèle...). Si l'on ne devait en retenir que deux, des outils comme celui de Mathforu ou encore https://www.airetriangle.com sont des services pratiques et utiles qui ne remplacent pas la connaissance des théorèmes et du cours, mais qui font gagner du temps dans la vérification des calculs.
Sachez enfin que Mathforu propose de nombreux autres outils que nous enrichissons sans cesse. Un forum pour les troisièmes est également accessible pour poser votre question sur les théorèmes dans les triangles ou tout autre sujet figurant au programme de mathématique de 3ème. Des modérateurs sont là pour vous répondre et vous accompagner dans la résolution de vos problèmes.
Toutes nos vidéos sur théorèmes dans les triangles