La loi des sinus

Pour la classe de 1ère S.

Enoncé complet et démonstration de la loi des sinus relation bien connue de proportionnalité entre les côtés d'un triangle et les sinus des angles opposés.

Avec exemples et exercices (pour l'instant non corrigés).

1. Notations traditionnelles

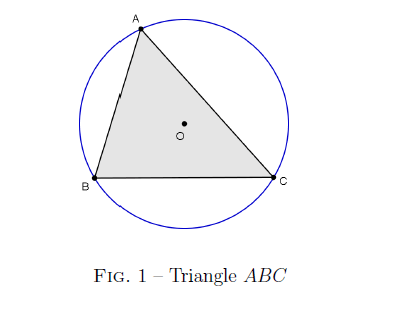
On rappelle ici les notations généralement employées pour désigner un certain nombres d’éléments dans un triangle $ABC$ .

Les longueurs des côtés $AB = c$ , $AC = b$ et $BC = a$ ;
Les mesures des angles $\widehat{A} = \widehat{BAC}$ , $\widehat{B} = \widehat{ABC}$ et $\widehat{C} = \widehat{ACB}$ ;
L’aire du triangle $A(ABC) = S$ ;
Le rayon du cercle circonscrit $OA = R$ .

On retiendra notamment que le côté opposé au sommet $A$ est désigné par la lettre $a$ , le côté opposé à $B$ est noté par $b$ et le côté opposé à $C$ est $c$ .

2 - La loi des sinus

On se propose d’établir le théorème affirmant que les côtés d’un triangle sont proportionnels aux sinus des angles opposés. Pour obtenir la forme la plus complète de cet énoncé, on considère deux configurations.

2.1 - Première configuration

Dans le triangle $ABC$ , on mène la hauteur $[CD]$ issue de $C$ ; deux cas de figure se produisent selon que cette hauteur est intérieure ou extérieure au triangle.

Dans le premier cas, on a $CD = AC \sin{\widehat{A}} = b \sin{\widehat{A}}$ et dans le second cas, on a $CD = AC sin(180-\widehat{A}) = b \sin{\widehat{A}}$ .

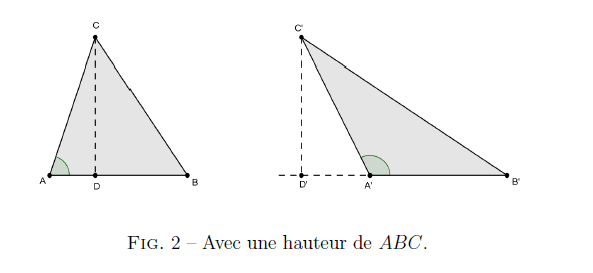
Dans les deux cas de figure, l’aire $S$ est donnée par $S = \dfrac{bc \sin{\widehat{A}}}{2}$

On en déduit par un raisonnement analogue les égalités

$\dfrac{ab \sin{\widehat{C}}}{2}= S =\dfrac{ac\sin{\widehat{B}}}{2}$

Ceci montre le fait important que l’aire du triangle peut être calculée avec deux côtés et le sinus de l’angle adjacent (on dit aussi l’angle compris).

On en déduit :

$2S = \dfrac{abc \sin{\widehat{A}}}{a} = \dfrac{abc \sin{\widehat{B}}}{b} = \dfrac{abc \sin{\widehat{C}}}{c}$

Et on obtient enfin alors cette forme de la loi des sinus :

$\boxed{\dfrac{a}{\sin{\widehat{A}}} = \dfrac{b}{\sin{\widehat{B}}} = \dfrac{c}{\sin{\widehat{C}}} = \dfrac{abc}{2S}}$ $(1)$

2.2 - Deuxième configuration

Dans le cercle circonscrit à $ABC$ , on trace le diamètre $[AZ]$ .

Deux cas sont à envisager selon que $Z$ est sur le même arc de cercle que $B$ , d’extrémités $A$ et $C$ , ou bien sur l’arc complémentaire.

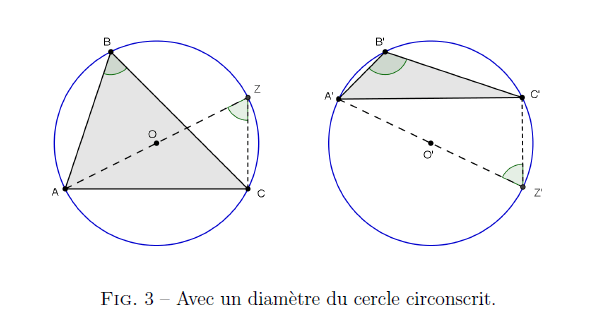
Dans le premier cas de figure, les angles inscrits $\widehat{B}$ et $\widehat{Z}$ sont égaux.

Dans le second cas de figure, les angles inscrits $\widehat{B}$ et $\widehat{Z}$ sont supplémentaires, et on a donc $\sin{\widehat{Z}} = \sin(180 -\widehat{B}) = \sin{\widehat{B}}$ .

En effet, il résulte du théorème de l’angle au centre que deux angles inscrits qui interceptent la même corde sont égaux ou bien supplémentaires.

Dans les deux cas, le triangle $AZC$ étant rectangle en $C$ , on en déduit $AZ = \dfrac{AC}{\sin{\widehat{Z}}}$

c’est-à-dire

$2R = \dfrac{b}{\sin{\widehat{B}}}$

Par un raisonnement en tout point similaire, on obtient ainsi:

$\dfrac{a}{\sin{\widehat{A}}}$ $= 2R =\dfrac{c}{\sin{\widehat{C}}}$

Ceci montre que le rayon du cercle circonscrit ne dépend que d’un côté et de l’angle opposé, c’est à dire de l’angle inscrit qui intercepte ce côté.

Il résulte de ces égalités la forme suivante de la loi des sinus :

$\boxed{\dfrac{a}{\sin{\widehat{A}}} = \dfrac{b}{\sin{\widehat{B}}} = \dfrac{c}{\sin{\widehat{C}}}=2R}$ $(2)$

2.3 - Énoncé de la loi des sinus

En regroupant les formules $(1)$ et $(2)$ , on est conduit à cet énoncé complet.

Théorème 1 (Loi des sinus).

Dans tout triangle, les côtés sont proportionnels aux sinus des angles opposés ; précisément, on a :

$\boxed{\dfrac{a}{\sin{\widehat{A}}} = \dfrac{b}{\sin{\widehat{B}}} = \dfrac{c}{\sin{\widehat{C}}}=\dfrac{abc}{2S} =2R}$

On rappelle que $S$ désigne l’aire du triangle, et $R$ le rayon de son cercle circonscrit.

Un corollaire immédiat du théorème 1 est la relation

$\boxed{abc = 4RS}$ . $(3)$

c’est-à-dire que le produit des trois côtés est égal à quatre fois le produit de l’aire et du rayon du cercle.

3 - Applications

3.1 - Exemples

Deux angles et le côté compris.

La loi des sinus permet de déterminer, dans un triangle, un côté ou bien un angle lorsque l’on connaît par exemple un côté et les deux angles qui lui sont adjacents. Cela correspond au premier cas d’isométrie des triangles.

Exemple 1.

Soit $ABC$ un triangle ; on donne $BC = 12$ , $\widehat{B} = 62^{\circ}$ et $\widehat{C} = 50^{\circ}$ .

Déterminer le troisième angle et les deux autres côtés.

Le troisième angle est $\widehat{A} = 68^{\circ}$ . On applique la loi de sinus, avec $a = 12$ ici :

$\boxed{\dfrac{12}{\sin{{68}}} = \dfrac{b}{\sin{{62}}} = \dfrac{c}{\sin{50}}}$

et ainsi on obtient : $b = 12 \times \dfrac{\sin{62}}{\sin{68}} \simeq \boxed{11{,}4}$ et $c = 12 \times \dfrac{\sin{50}}{\sin{68}} \simeq \boxed{9{,}9}$ avec des arrondis au dixième.

Deux côtés et l’angle non compris.

Dans certains cas de figure, on peut calculer les éléments manquants lorsque sont donnés deux côtés et un angle opposé à l’un d’eux.

Exemple 2.

Soit $ABC$ un triangle ; on donne $BC = 25$ , $AC = 36$ et $\widehat{B} = 72^{\circ}$ .

Déterminer le troisième côté et les deux autres angles.

Dans ce cas, où $a = 25$ et $b = 36$ , la loi des sinus s’écrit

$\boxed{\dfrac{25}{\sin{\widehat{A}}} = \dfrac{36}{\sin{\widehat{72}}} = \dfrac{c}{\sin{\widehat{C}}}}$

d’où on tire :
$\sin{\widehat{A}} = \sin{72} \times \dfrac{25}{36}$ , soit $\widehat{A} \simeq 41^{\circ}$ et on en déduit le troisième angle $\widehat{C} \simeq 67^{\circ}$ , les mesures des angles étant arrondies au degré.

Alors, la loi des sinus permet le calcul du troisième côté
$c = 36 \times \dfrac{\sin{67}}{\sin{72}} \simeq \boxed{34{,}8}$ valeur arrondie au dixième.

3.2 - Exercices

Exercice 1. Dans un triangle $ABC$ , on a $BC = 8$ , $\widehat{B} = 50^{\circ}$ , $\widehat{C} = 110^{\circ}$ .
Déterminer les éléments manquants.
Exercice 2. Dans un triangle $ABC$ , on a $BC = 7$ , $\widehat{B} = 50^{\circ}$ , $\widehat{A} = 80^{\circ}$ .
Déterminer les éléments manquants.
Exercice 3. Dans un triangle $ABC$ , on a $BC = 25$ , $AC = 10$ et $\widehat{C} = 80^{\circ}$ .
Déterminer les éléments manquants.
Exercice 4. Dans un triangle $ABC$ , on a $BC = 7{,} 5$ , $AC = 10$ et $\widehat{C}= 42^{\circ}$ .
Déterminer les éléments manquants.
Exercice 5. Dans un triangle $ABC$ , on a $BC = 36$ , $\widehat{B} = 45^{\circ}$ et $\widehat{C}= 62^{\circ}$ .
Déterminer l’aire de $ABC$ .
Exercice 6. Soit $ABCD$ un quadrilatère convexe, dans lequel on donne les longueurs $AB = 20$ , $AC = 40$ et $CD = 30$ , ainsi que les angles $\widehat{BAC} = 60^{\circ}$ et $\widehat{ACD} = 45^{\circ}$ .
Déterminer l’aire de $ABCD$ .
Exercice 7 (Calcul d’une hauteur « inaccessible »). Soit $ABC$ un triangle ayant l’angle $\widehat{B}$ obtus), tel que $AB = 50$ , $\widehat{BAC} = 74^{\circ}$ et $\widehat{HBC} = 81^{\circ}$ . Soit $H$ le projeté orthogonal de $C$ sur $(AB)$ .
Déterminer la hauteur $CH$ .
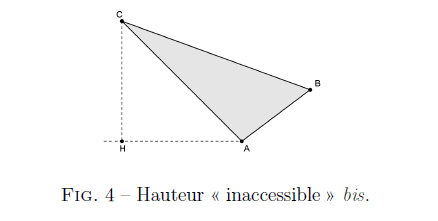
Exercice 8 (Calcul d’une hauteur « inaccessible » bis). Sur la figure $(4)$ , on donne $\widehat{HAC} = 42^{\circ}$ , $\widehat{A} = 105^{\circ}$ , $\widehat{B} = 36^{\circ}$ et $AB = 300$ .
Déterminer $CH$ .

Exercice 9.
Dans un triangle $ABC$ , avec les notations usuelles, montrer que $a = b \cos{\widehat{C}} + c \cos{\widehat{B}}$ pour en déduire la formule d’addition : $\sin{\widehat{B} +\widehat{C}} = \sin{\widehat{B}} \cos{\widehat{C}} + \sin{\widehat{C}} \cos{\widehat{B}}$ .

Remarque.
Dans La trigonométrie (ouvrage hélàs difficile à se procurer...) de Robert Campbell (Que-sais-je no 692, 1956), on trouve des applications de la loi des sinus à l’astronomie, pour déterminer la distance Terre-Lune, la distance Terre-Soleil (par le procédé de Halley) et la distance entre la Terre et une autre étoile.

Par Zauctore