Angles et cercles en Troisième

Pour la classe de Troisième : les théorèmes sur les angles dans le cercle.

Plan de cours

• Théorème de l'angle au centre
• Théorème des angles inscrits
• Propriété du quadrilatère inscrit
• Propriété de la tangente.

Cours

Théorème 1.

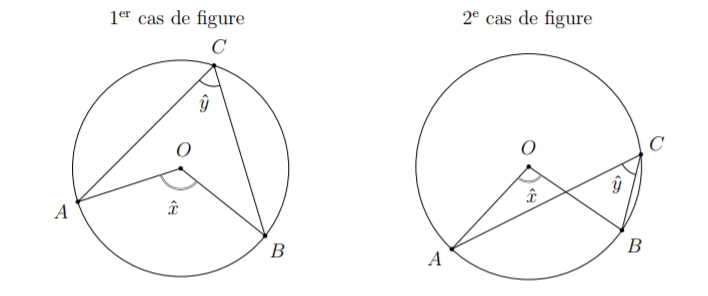
Tab. 1 – Le théorème de l’angle au centre : $\widehat{x} = 2 \times \widehat{y}$.

Preuve du théorème.

[Se reporter aux figures Tab. 2]

La première partie de la preuve concerne le cas de figure où le centre $O$ est contenu dans l’angle $\widehat{ACB}$. Soit $C'$ le point diamétralement opposé à $C$ sur le cercle.

Alors le triangle $ACC'$ est rectangle en $A$. Alors $\widehat{AOC'}$ est le supplément de $\widehat{AOC}$, c’est-à-dire $\widehat{AOC'} = 180 - \widehat{AOC}$.

De plus, dans le triangle $AOC$ isocèle en $O$, on a :

$\widehat{AOC} = 180 - \widehat{ACO} - \widehat{CAO} = 180 - 2 \times \widehat{ACO}$.

On en déduit donc que :

$\widehat{AOC'} = 180 - \widehat{AOC} = 180 - (180 - 2 \times \widehat{ACO}) = 2 \times \widehat{ACO}$.

Ceci montre le théorème de l’angle au centre dans le cas particulier où l’un des côtés est un diamètre du cercle.

Le triangle $CBC'$ étant rectangle en $B$, on a donc aussi :

$\widehat{C'OB} = 2 \times \widehat{C'CB}$.

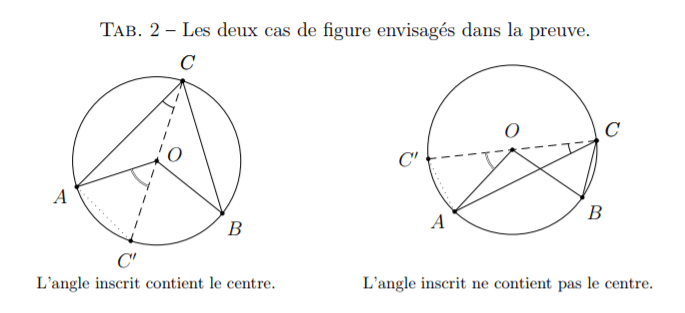
Puisque les angles $\widehat{AOC'}$ et $\widehat{C'OB}$ sont adjacents, tout comme les angles $\widehat{ACC'}$ et $\widehat{C'CB}$, on en déduit que :

$\widehat{AOB} = \widehat{AOC'} + \widehat{C'OB} = 2 \widehat{ACC'} + 2 \widehat{C'CB} = 2 \widehat{ACB}$.

Le deuxième cas de figure est celui où le centre est hors de l’angle $\widehat{ACB}$. Avec le diamètre $[CC']$, on a successivement :

$\widehat{C'OA} = 2 \times \widehat{C'CA}$ et $\widehat{C'OB} = 2 \times \widehat{C'CB}$,

$\widehat{AOB} = \widehat{C'OB} - \widehat{C'OA} = 2 \times (\widehat {C'CB} - \widehat{C'CA}) = 2 \times \widehat{ACB}$.

Corollaire 1.

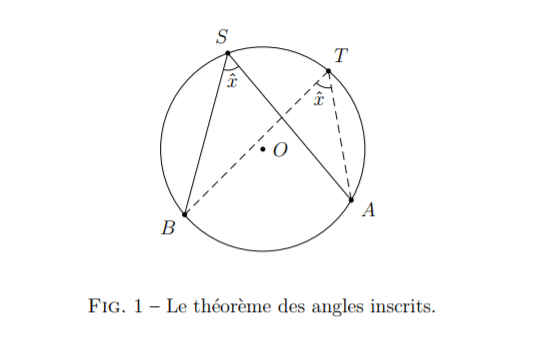
Démonstration.

D’après le théorème de l’angle au centre, puisque les angles inscrits $\widehat{ASB}$ et $\widehat{ATB}$ interceptent le même arc que l’angle au centre $\widehat{AOB}$, on a :

$2 \times \widehat{ASB} = \widehat{AOB} = 2 \times \widehat{ATB}$.

Vocabulaire

Corollaire 2.

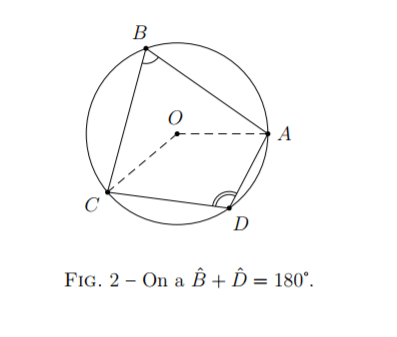
Preuve rapide.

Le théorème de l’angle au centre et l’angle plein autour du point $O$ donnent :

$2 \times \widehat{ASB} + 2 \times \widehat{ATB} = 360$°,

d’où $\widehat{ASB} + \widehat{ATB} = 180$˚.

Corollaire 3.

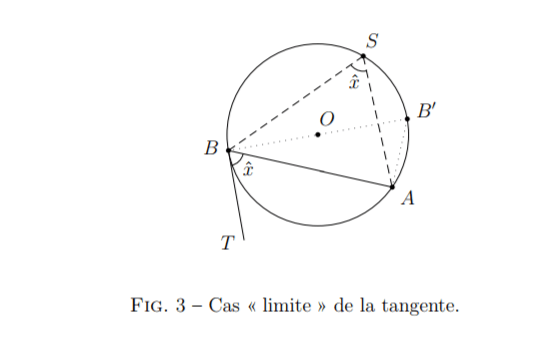
Preuve rapide.

Avec le diamètre $[BB']$, les angles $\widehat{B'BT}$ et $\widehat{B'AB}$ sont droits.

On voit donc que les angles $\widehat{ABT}$ et $\widehat{AB'B}$ ont le même complémentaire $\widehat{BB'A}$ ; ils sont donc égaux :

$\widehat{ABT} = \widehat{AB'B} = \widehat{ASB}$.

Par Zauctore

Toutes nos vidéos sur théorèmes de l'angle au centre, des angles inscrits

@youtube