Théorèmes de l'angle droit et du demi-cercle en Quatrième

Pour la classe de Quatrième, une courte leçon montrant le lien entre les triangles rectangles et les demi-cercles : propriétés directes et réciproque pour une caractérisation des angles droits.

Théorème 1

Démonstration

Le triangle $ABC$ est en fait un demi-rectangle $ABA′C$, de centre $O$.

On sait que les diagonales d’un rectangle sont égales et ont le même milieu, ici $O$ ; on en déduit donc que $OA = OB = OC$, ce qui démontre que le cercle de centre $O$ passant par $A$ passe aussi par $B$ et par $C$.

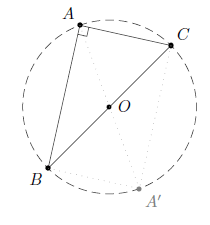
Corollaire 1

Le cercle ayant l’hypoténuse pour diamètre passe par le sommet de l’angle droit.

Corollaire 2

Le milieu de l’hypoténuse est équidistant des trois sommets.

Théorème 2

Démonstration

En plaçant le point $A'$ diamétralement opposé à $A$ sur le cercle, on forme un quadrilatère $ABA'C$ dont les diagonales $[AA']$ et $[BC]$

• ont le même milieu $O$

• sont égales ;

C’est donc un rectangle.

Ceci montre que l’angle $\widehat{BAC}$ est droit.

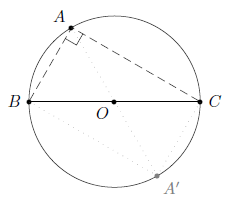
Corollaire 3

Le triangle formé par un diamètre et un point du cercle est rectangle en celui-ci.

Toutes nos vidéos sur théorèmes de l'angle droit et du demi-cercle