|
|
| 1ère: Réprésenter graphiquement les termes d'une suite |
|
| |
|
|
Transmis par Zorro,
le Mardi 29 Janvier 2008 : 13035 lectures. |
 |
Cette fiche permet de comprendre comment :
- représenter graphiquement les premiers termes d'une suite définie par récurrence par une relation du type Un+1 = f(Un)
- se servir de cette représentation graphique pour conjecturer le comportement d'une telle suite quant à sa convergence
Pour conjecturer le comportement d'une suite définie à l'aide d'une fonction f par Un+1 = f(Un), on trace dans un repère :
Cf la courbe représentative de f (en bleu sur l'image)
la droite (d) d'équation y = x (en noir sur l'image).
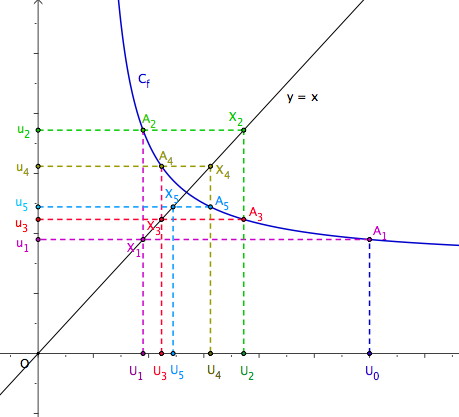
On place, sur l'axe des abscisses, le point de coordonnées (U0 ; 0) représentant le premier terme de la suite.
Pour trouver U1 = f(U0) il faut lire l'ordonnée du point A1 de la courbe Cf.
Le point X1 de la droite (d) a donc pour coordonnées (U1 ; U1).
Pour trouver U2 = f(U1) il faut lire l'ordonnée du point A2 de la courbe Cf.
Et ainsi de suite ...... on trouve les autres termes de la suite.
Dans le cas présenté, on peut conjecturer que la suite (Un) possède une limite réelle l qui est l'abscisse du point d'intersection de Cf et de (d).
Pour trouver la valeur de l, il faudra résoudre l'équation : f(l) = l
Au passage, on peut vérifier, sur cet exemple, qu'une suite construite à l'aide d'une fonction décroissante n'est pas forcément décroissante.
En effet, sur l'intervalle présenté, la fonction f est décroissante et les nombres U0 , U1 , U2 , U3 , U4 et U5 ne sont pas rangés dans l'ordre inverse de leur rang. (Regarder les emplacements sur l'axe des abscisses).
|
|
|
|
|
| Boîte de connexion |
 Bienvenue invité
Inscris-toi c'est gratuit !
 
Rejoins-nous afin de poser tes questions dans les forums de Math foru' :
 Crée ton compte | | | |  Connexion :
|
| | | | | |
|
| |
|
Partager sur Facebook
Partager sur Twitter
Envoyer par e-mail