Factorisation et étude de signes en 2nd

I. Signe d'une fonction affine

Propriété :
Soient $a$ et $b$ deux nombres réels avec $a$ différent de $0$ .
La fonction affine définie $f(x) = ax + b$ s'annule et change de signe une fois dans son domaine de définition pour $x=-\dfrac{b}{a}$ .
• Si $a$ est positif, la fonction est négative puis positive.
• Si $a$ est négatif, la fonction est positive puis négative.

Représentation graphique :
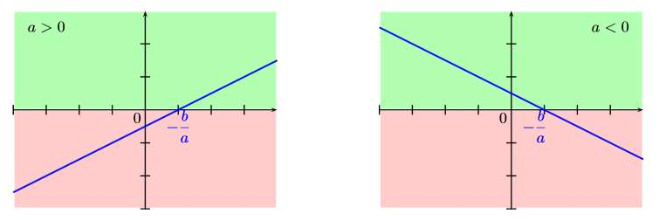
tableau-de-signes
Voici les tableaux de signes correspondants à ces deux représentations graphiques :
Cas où $a$ est positif :

Cas où $a$ est négatif :

Exemple :
Dresser le tableau de signes de la fonction $f$ définie sur $\mathbb R$ par $f(x)=-5x+11$ .
On remarque ici que $a=-5<0$ . On est dans le deuxième cas.
Recherche de la valeur qui annule la fonction :

$-5x+11=0\Longleftrightarrow x =\dfrac{-11}{-5}=\dfrac{11}{5}$

II. Factorisation

Rappels des méthodes de factorisation :

Pour $a$ , $b$ et $k$ trois réels : $ka+kb=k(a+b)$ ;
Utilisation des identités remarquables :

$a^2-b^2=(a+b)(a-b)$

$a^2+b^2+2ab=(a+b)^2$

$a^2+b^2-2ab=(a-b)^2$

III. Signe du produit de deux fonctions affines

Propriété "Règle des signes" :

Le produit de deux nombres de même signe est positif.
Le produit de deux nombres de signes différents est négatif.

Méthode d'étude du signe d'un produit :
Résoudre l'inéquation

$(x+12)(4x+16)\geq 0$

Etape 1 : on résout séparemment chaque équation.
- $x+12=0\Longleftrightarrow x=-12$
- $4x+16\Longleftrightarrow x=-4$
Etape 2 : on fait un tableau de signe où on indique sur la première ligne les bornes de l'ensemble de définition et les solutions trouvées à l'étape 1.
Etape 3 : on utilise ce que nous avons appris sur le signe d'une fonction affine (voir I.) en complétant les 2ème et 3ème lignes pour $x +12$ et $4x+16$ séparément.
Etape 4 : on utilise la règle des signes de deux nombres relatifs (rappelée ci-dessus) en remplissant la dernière ligne.
Etape 5 : on conclut sur l'ensemble des solutions. Ici on veut résoudre $(x+12)(4x+16)\geq0$ donc on cherche sur la dernière ligne le(s) intervalle(s) où le produit est positif (c'est-à-dire avec un signe "+").

Voici le tableau de signe fini :

IV. Signe d'une fonction homographique

Définition :
On appelle fonction homographique toute fonction f qui peut s'écrire sous la forme du quotient de fonctions affines.
Soient $a$ , $b$ , $c$ et $d$ quatre nombres réels tels que $ad-bc\neq 0$ et $c\neq 0$ :

$f(x)=\dfrac{ax+b}{cx+d}$

Propriété :
Une fonction homographique est définie sur $\mathbb R$ privé de la valeur qui annule son dénominateur dite valeur interdite.
Sa courbe représentative est une hyperbole qui comporte deux branches disjointes.

On représente ci-dessous la fonction $f$ définie par :

$f(x)=\dfrac{x+1}{6x-12}$

La valeur interdite est $2$ car elle annule $6x-12$ .
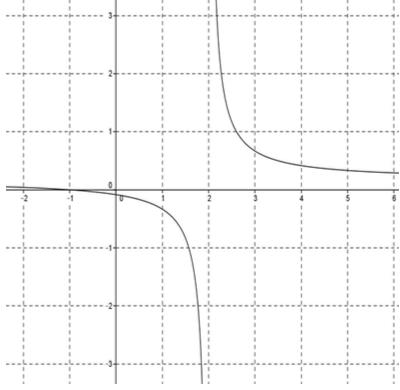
graphique

Méthode d'étude du signe d'un quotient :
Résoudre l'inéquation :

$\dfrac{3x-5}{2x+7}\leq 0$

Etape 1 : on résout séparément chaque équation
- $3x-5=0\Longleftrightarrow x=\dfrac{5}{3}$ ;
- $2x+7=0\Longleftrightarrow x=-\dfrac{7}{2}$ ;
Etape 2 : on fait un tableau de signe où on indique sur la première ligne les bornes de l'ensemble de définition et les solutions trouvées à l'étape 1.
Etape 3 : on utilise ce que nous avons appris sur le signe d'une fonction affine (voir I.) en complétant les 2ème et 3ème lignes pour $3x-5$ et $2x + 7$ séparément.
Etape 4 : on utilise la propriété "règle des signes" du quotient de deux nombres relatifs (similaire à celle du produit rappelée ci-dessus) en remplissant la dernière ligne.
Attention !! On indique la valeur interdite par une double barre sur la dernière ligne.
Etape 5 : on conclut sur l'ensemble des solutions.
Ici on veut résoudre $\dfrac{3x-5}{2x+7}\leq 0$ , donc on cherche sur la dernière ligne $2x + 7$ le(s) intervalle(s) où le quotient est négatif (c'est-à-dire avec un signe $"-"$ ).

Voici le tableau fini :
tableau

Factorisation et étude de signes en 2nd

I. Signe d'une fonction affine

II. Factorisation

III. Signe du produit de deux fonctions affines

IV. Signe d'une fonction homographique

Posez vos questions

Fiches méthodes

Cours de mathématiques de seconde