Généralités sur les fonctions en 2nd

I. Notion de fonctions

Remarques :

• Chaque nombre $x$ de l'ensemble $D$ a une unique image par $f$.
• Chaque nombre $y$ peut avoir plusieurs, un seul ou aucun antécédent(s).
• L'ensemble de définition $D$ peut être l'ensemble des nombres réels (c'est-à-dire l'ensemble des nombres connus $(0;5;-2{,}3;-7;\sqrt 2;\pi)$ noté $\mathbb R$ , ou être constitué d'une ou plusieurs parties de $\mathbb R$ comme des intervalles de $\mathbb R$.

Voici quelques exemples d'intervalles de $\mathbb R$ :

Encadrement/Comparaison	Notation de l'intervalle	Représentation graphique
$1\leq x\leq 2$	$x\in\lbrack 1;2\rbrack$
$3$	$x\in\rbrack 3;7\lbrack$
$x\geq 4$	$x\in\lbrack 4;+\infty\lbrack$
$x<5$	$x\in\rbrack -\infty;5\lbrack$

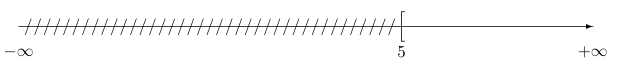II. Différentes représentations d'une fonction

Il existe plusieurs façons de présenter une fonction : une expression algébrique , un tableau de valeurs ou une courbe.

1. Avec une expression algébrique

Soit $f$ une fonction définie sur $D$ et $x\in D$. L'expression algébrique d'une fonction donne directement $f(x)$ en fonction de $x$ comme un programme de calcul.

Exemple : soit $f$ une fonction définie par le programme de calcul suivant :

La fonction liée au programme est : $f(x)=(x-4)^2$

Exemples de calculs d'images/d'antécédents d'un nombre :
Soit $f$ la fonction définie sur $\mathbb R$ par : $f(x)= -3x + 5$

• Calculer l'image de $-1$ et de $4$ par $f$.

$f (-1)=-3\times (-1)+ 5=3+ 5=8$
L'image de $-1$ par $f$ est $8$.
$f (4)=-3\times 4+ 5=-12+ 5=-7$
L'image de $4$ par $f$ est $-7$.

• Calculer, s'il en existe, le ou les antécédents par $f$ de $23$.

C'est-à-dire, ici :

$\begin{array}{ccc} -3x + 5 &=& 23\\ -3x &=& 18\\ x &=& \dfrac{18}{-3}\\ x &=& -6 \end{array}$

L'antécédent de $23$ par $f$ est $-6$.

2. Avec un tableau

Un tableau de valeurs d'une fonction donne sur la première ligne différentes valeurs de $x$ et associe à chacun une unique image sur la deuxième ligne.

Exemple :
Avant une compétition, on effectue une pesée de boxeurs numérotés de 1 à 8. Le tableau suivant indique les résultats obtenus :

On définit ainsi une fonction $f$ associant à chaque numéro de boxeur son poids.

1. L'ensemble de définition de la fonction $f$ est $\{1;8\}$
   Remarque : ici, l'ensemble de définition n'est pas un intervalle mais un ensemble fini.
2. L'image de $3$ par la fonction $f$ est $69$.
   L'image de $6$ par la fonction $f$ est $73$.
3. Les antécédents de $70$ sont $4$ et $8$.

3. Avec une courbe

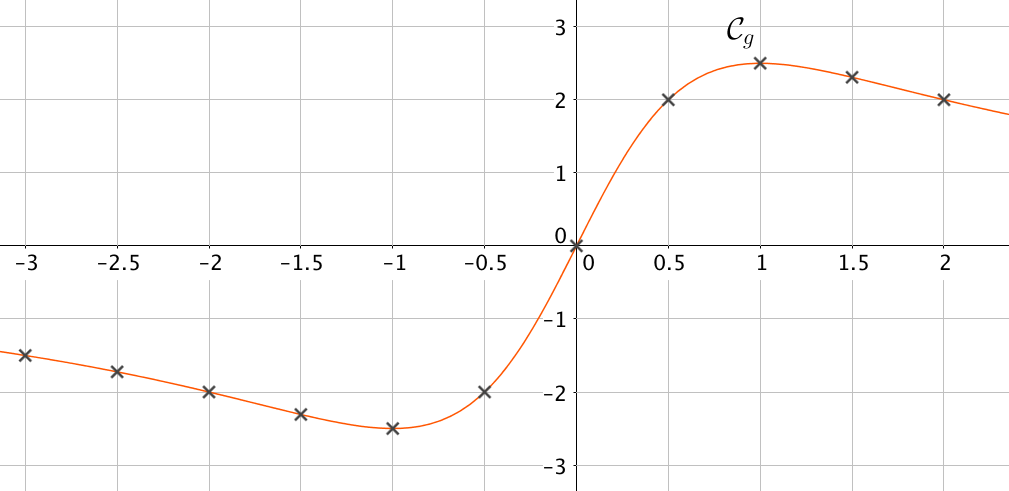
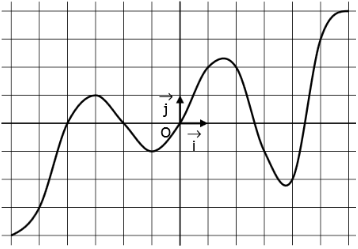
Exemple :
On donne ci-contre la représentation graphique d'une fonction $f$ définie sur l'intervalle $\lbrack -6 ; 6\rbrack$.

Pour lire l'image d'un nombre, on place $x$ sur l'axe des abscisses puis on se déplace verticalement pour rencontrer $\mathcal C_f$ et on lit $f(x)$ sur l'axe des ordonnées.

L'image de $5$ est $3$ et l'image de $-2$ est $0$.

Pour trouver le ou le antécédents d'un nombre, on trace une droite horizontale passant par cette valeur sur l'axe des ordonnées puis à partir des points d'intersection on se déplace verticalement vers l'axe des abscisses pour lire les antécédents.

D'après le graphique, l'antécédents de $-3$ est $-5$ et les antécédents de $2$ sont : $1$, $2$ et $\approx 4{,}7$.

Lien avec une expression algébrique : On considère la fonction $g$ définie sur $\mathbb R$ par: $g(x)=\dfrac{5x}{x^2+1}$.

On souhaite tracer la portion de la courbe représentative de cette fonction sur l'intervalle $\lbrack -3;2\rbrack$.

• On commence par compléter un tableau de valeurs :

• Puis on place les points de coordonnées $(x ; g(x))$ dans un repère qu'on relie à la main. (On pourra s'aider de la calculatrice pour visualiser l'allure de la représentation graphique.)