Fonctions de référence : fonction carrée et fonction inverse

I. La fonction carré

Définition n°1 :

La fonction $f$ définie sur $\mathbb{R}$ par : $f(x) = x^2$ s'appelle la fonction carré.

Propriété n°1 :

La fonction carré est strictement décroissante sur $]-\infty; 0]$ et strictement croissante sur $[0 ; +\infty[$ .

Tableau de variations :

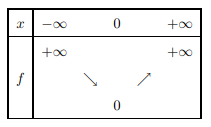
var carrée

Représentation graphique :

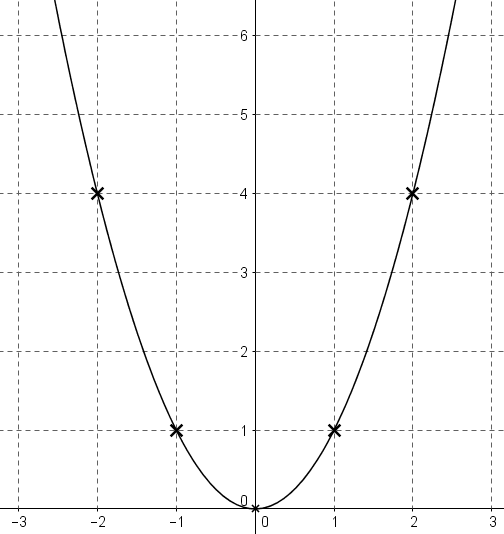
courbe carrée

Remarques :

Dans un repère $(O ; I, J)$ , la courbe représentative de la fonction carrée est une parabole de sommet $O$ .
Dans un repère orthogonal, la courbe de la fonction carrée admet l'axe des ordonnées pour axe de symétrie.

$\quad$

II. La fonction inverse

Définition n°2 :

La fonction $f$ définie sur $\mathbb{R}^* =$ $]-\infty ; 0[$ $\cup$ $]0 ; +\infty[$ par : $f(x) = \frac{1}{x}$ est appelée fonction inverse.

Propriété n°2 :

La fonction inverse est strictement décroissante sur $]-\infty ; 0[$ et sur $]0 ; +\infty[$ .

Remarque : Attention, on ne peut pas dire que la fonction inverse est décroissante sur $]-\infty ; 0[$ $\cup$ $]0 ; +\infty[$ car $]-\infty ; 0[$ $\cup$ $]0 ; +\infty[$ n'est pas un intervalle.

Tableau de variations :

Tableau variations fonction inverse

Représentation graphique :

Imgur

Remarques :

Dans un repère $(O ; I, J)$ , la courbe représentative de la fonction inverse est une hyperbole de centre $O$ .
Cette hyperbole admet l'origine $O$ du repère comme centre de symétrie.

Fonctions de référence : fonction carrée et fonction inverse

I. La fonction carré

II. La fonction inverse

Toutes nos vidéos sur fonctions de référence : fonction carrée et fonction inverse

Posez vos questions

Fiches méthodes

Cours de mathématiques de seconde