Statistiques descriptives en 2nd
I. Vocabulaire, effectifs et fréquences
Vocabulaire :
L'ensemble sur lequel porte une étude statistique est appelé population. Par exemple, l'ensemble des élèves de la classe, l'ensemble des habitants de France...
Un élément de la population est appelé individu.
La propriété étudiée sur chaque individu est appelée caractère.
Les différentes valeurs prises par le caractère sont appelées modalités.
Lorsque les modalités ne sont que des valeurs numériques, le caractère est dit quantitatif.
On distingue deux cas :
- Le caractère est dit quantitatif discret s'il ne peut prendre que des modalités isolées. Par exemple, on peut étudier le nombre de frères sœurs, qui ne pourra prendre que les modalités 0 ; 1 ; 2 ; 3...
- Le caractère est dit quantitatif continu si les valeurs sont prises dans un intervalle de . Ces intervalles sont appelés classes.
Par exemple, on peut étudier la taille des élèves d'un lycée. Les valeurs de ce caractère sont regroupés en classes : - Dans le cas où les modalités ne sont pas des valeurs numériques, le caractère est dit qualitatif. Par exemple, étudier la couleur des yeux ou le sport pratiqué...
Faire des statistiques, c’est recueillir, organiser, synthétiser, représenter et exploiter des données, numériques ou non, dans un but de comparaison, de prévision, de constat...
Les métiers où les statistiques sont beaucoup utilisées sont les assureurs (risques d’accidents, de maladie des assurés), les médecins (épidémiologie), les démographes (populations et leur dynamique), les économistes (emploi, conjoncture économique), les météorologues...
Définitions n°1 :
- On appelle effectif total le nombre d'individus dans la population.
- L'effectif d'une modalité est le nombre d'individus de la population dont le caractère prend cette modalité.
- A chaque modalité (ou classe) est associée une fréquence f. C'est le quotient de l'effectif de cette modalité par l'effectif total :
Remarques :
- Une fréquence est un nombre compris entre 0 et 1.
- La somme des fréquences de toutes les modalités est égale à 1.
Exemple 1 :
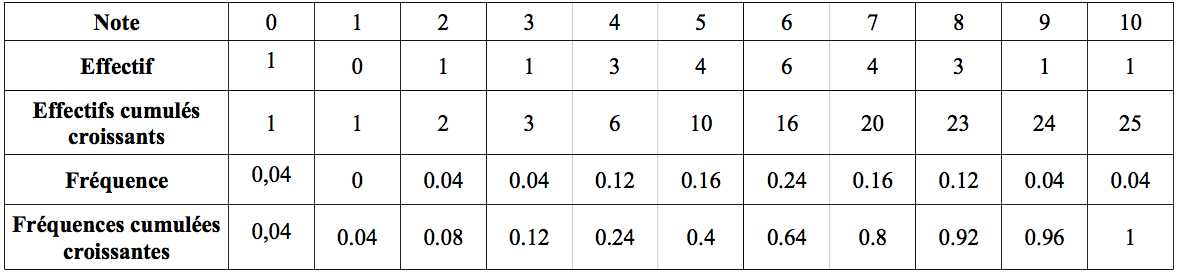
Voici les notes obtenues à un contrôle (sur 10) dans une classe de 25 élèves : (notée Série A)
On peut représenter cette série par un tableau d’effectifs, et le compléter par le calcul des fréquences :
Exemple 2 :
On va utiliser ici un regroupement par classe, ce qui rend l'étude moins précise, mais qui permet d'avoir une vision globale de la situation.
Une enquête réalisée sur 200 personnes indique le temps passé devant la télévision chaque jour.
Les données sont regroupées dans le tableau suivant (notée série B) :
Définition n°2 :
Dans le cas d'un caractère quantitatif, on peut ordonner les différentes modalités de la plus petite à la plus grande (ou de la plus grande à la plus petite) puis additionner les effectifs successifs : on obtient les effectifs cumulés croissants (ou décroissants).
On obtient de la même façon les fréquences cumulées croissantes (ou décroissantes).
Exemple :
On travaille avec la série A.
- Compléter le tableau des effectifs cumulés croissants et des fréquences cumulées croissantes.
- Combien d'élèves ont une note inférieure ou égale à 6 ?
- Quelle est la proportion (exprimée en pourcentages) d'élèves n'ayant pas obtenu la moyenne ?
Solution :
- On lit dans le tableau que 16 élèves ont une note inférieure ou égale à 6.
- On lit 0,24. Donc 24% des élèves n'ont pas eu la moyenne.
II. Caractéristiques de position d'une série statistique
Définition n°3 :
La moyenne d'une série statistique, notéē , est égale à la somme totale des valeurs prises par le caractère divisée par l'effectif total.
Exemple : Calculer la moyenne de la série A.
La moyenne de la classe est de .
Exemple 2 : Calculer la moyenne de la série B.
Lorsque la série est regroupée en classes, on prend pour valeurs dans le calcul de la moyenne le centre de chaque classe. Par exemple, le centre de la classe est :
On calcule :
Le temps moyen est de heures, soit heures et minutes. (Conversion : ).
Propriété :
Si désignent les modalités d'une série statistique, et désignent les fréquences correspondantes, alors :
Exemple :
On a demandé aux élèves d'une classe d'indiquer le nombre de frères et sœurs qu'ils ont. Voici les résultats (série C) :
Calculer le nombre moyen de frères et sœurs qu'a chaque élève.
Le nombre moyen de frères et sœurs d'un élève de la classe est de .
Définition n°4 :
Dans une série statistique ordonnée, la médiane, notée , est un nombre qui permet de partager cette série en deux sous-groupes de même effectif.
Méthode :
On commence par ordonner la série, puis on la partage en deux sous-groupes de même effectif.
- Si l'effectif total est impair, alors il restera une valeur entre les deux sous-groupes de même effectif. Cette valeur sera
la médiane. - Si l'effectif total est pair, on choisira pour médiane la moyenne des nombres situés « au milieu » de la série.
Exemple :
Dans un groupe de élèves, voici les notes (sur ) obtenues à un devoir de mathématiques (série D):
12 ; 4 ; 16 ; 16 ; 10 ; 7 ; 9 ; 12 ; 9 ; 12.On range puis on partage la série :
Ici l'effectif total est qui est un nombre pair. On a deux sous-groupes de valeurs. La médiane est la moyenne de la 5ème et 6ème valeur :
Interprétation :
La moitié des élèves a eu plus que 11 et l'autre moitié moins que 11.
Définitions n°5 :
- On appelle premier quartile d'une série statistique, noté , la plus petite valeur de cette série telle qu'au moins des valeurs de la série lui soient inférieures ou égales.
- On appelle troisième quartile d'une série statistique, noté , la plus petite valeur de cette série telle qu'au moins des valeurs de la série lui soient inférieures ou égales.
Méthode :
Pour une série ordonnée d'effectif total :
- On détermine l'arrondi de à l'entier supérieur et on obtient le rang de dans la série.
• On détermine l'arrondi de à l'entier supérieur et on obtient le rang de dans la série.
Exemple n°1 :
On reprend la série précédente (série D) ordonnée:
L'effectif total est .
On calcule : donc est la 3ème valeur de la série ordonnée. (Attention n'est pas égal à ou à )
Interprétation :
Au moins des élèves ont eu une note inférieure ou égale à .On calcule : donc est la 8ème valeur de la série ordonnée.
Interprétation :
Au moins des élèves ont eu une note inférieure ou égale à .
Exemple n°2 : utilisation des fréquences cumulées croissantes
On reprend la série A.
On a dépassé les pour la valeur donc :
On a dépassé les pour la valeur donc :
III. Caractéristiques de dispersion d'une série statistique
Définition n°6 :
On appelle étendue d'une série statistique la différence, notée , entre la plus grande et la plus petite valeur de la série.
Exemple :
Pour la série D, la plus grande valeur est et la plus petite est . Donc :
Définition n°7 :
On appelle écart interquartile d'une série statistique le nombre .
Remarque :
L’écart interquartile mesure la dispersion des valeurs autour de la médiane :
Plus l’écart est petit, plus les valeurs de la série appartenant à l’intervalle interquartile sont concentrées autour de la médiane.
Exemple :
Pour la série D, on a : et . Donc l'écart interquartile de cette série est :
IV. Représentations graphiques
1. Nuage de points
Lorsque le caractère étudié est quantitatif et discret, on peut représenter la série par un nuage de points.
C'est l'ensemble des points placés dans un repère dont les abscisses sont les valeurs du caractère et les ordonnées sont les effectifs correspondants.

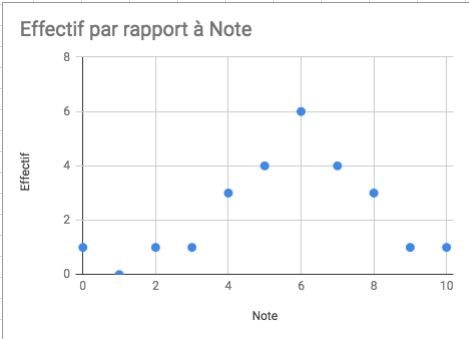
2. L'histogramme
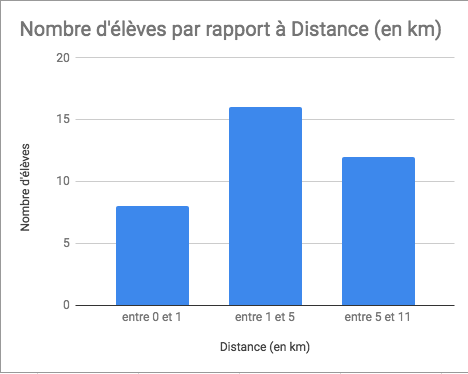
Lorsque le caractère est quantitatif et que les modalités sont regroupées en classes, on peut représenter la série par un histogramme.
L'aire de chaque rectangle est proportionnelle à l'effectif de chaque classe.
Lorsque les classes ont la même amplitude, la hauteur du rectangle est proportionnelle aux effectifs.
On considère le tableau suivant qui donne la distance entre le domicile et le lycée pour les élèves d'une classe.