Les angles
I. Notation et définition
Définition :
Un angle est une portion du plan (feuille) délimitée par deux demi-droites ayant le même point comme origine.
Les deux demi-droites sont appelées côtés de l'angle.
Leur origine est appelée le sommet de l'angle.
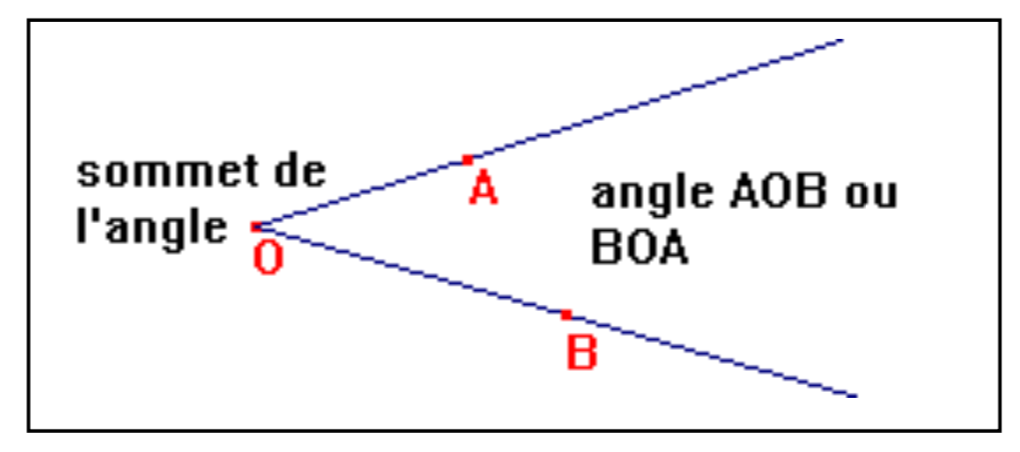
Lorsque l'on écrit un angle avec trois lettres (comme dans la figure ci-dessus), il faut toujours écrire le sommet de l'angle au milieu des autres lettres.
II. Mesures associées
Afin de pouvoir comparer des angles, on associe à chacun une mesure d’angle. On utilise un rapporteur pour déterminer la mesure d’un angle.
- On place le centre du rapporteur sur le sommet de l’angle ;
- On place le rapporteur de sorte que le zéro du rapporteur soit sur une des demi-droites formant l’angle ;
- On lit le nombre par lequel passe la deuxième demi-droite sur le rapporteur ;
- L’unité de mesure des angles est le degré noté °.
Attention :
Il faut parfois prolonger les demi-droites !
Exemple :
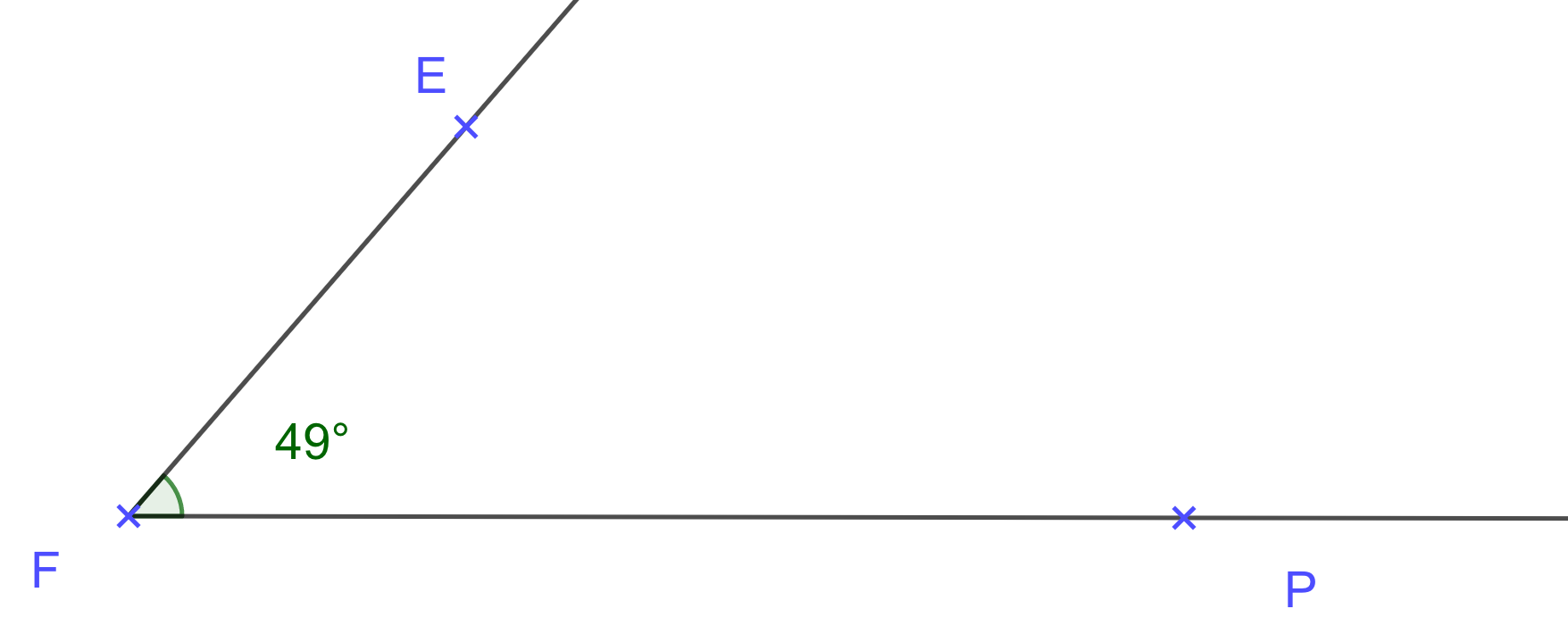
Vous pouvez modifier la mesure de l'angle en bougeant un des points.
III. Cas particuliers
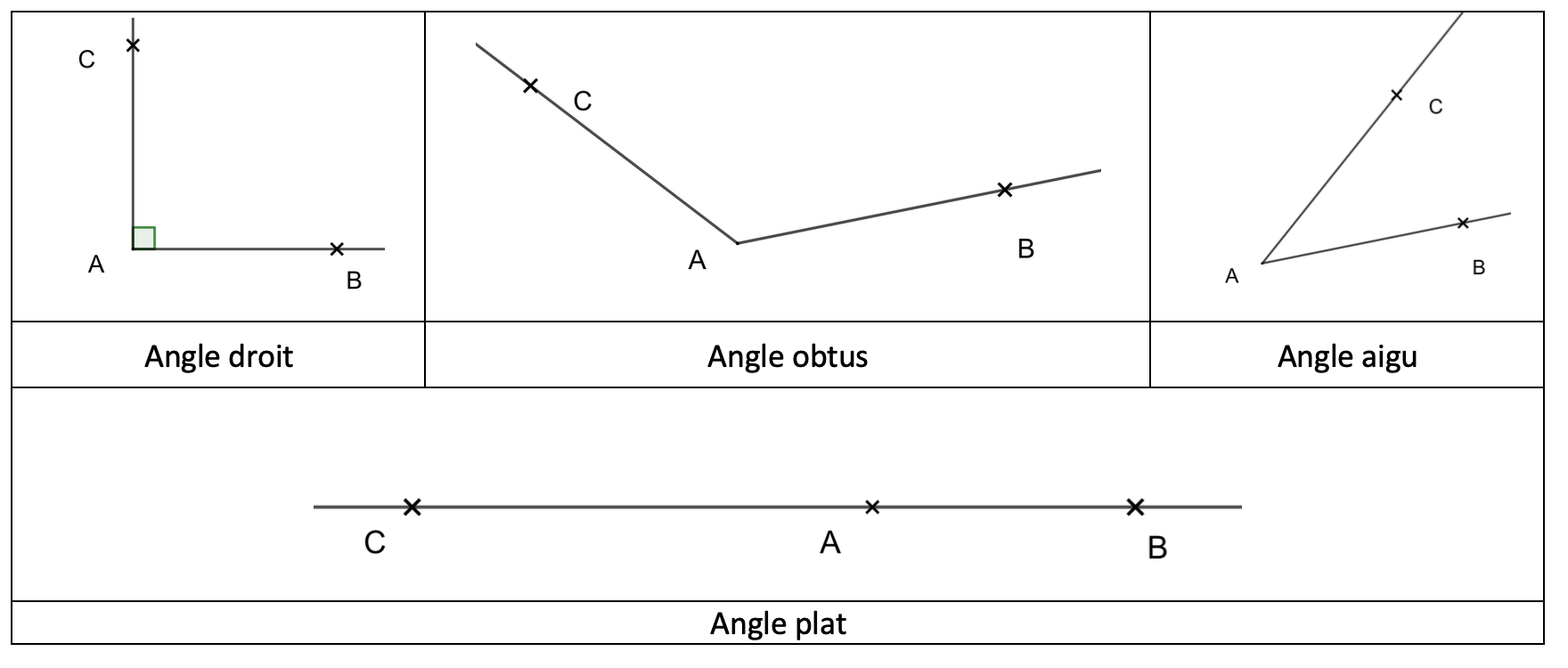
- Un angle droit est formé de 2 demi-droites perpendiculaires. Sa mesure sur le rapporteur est de 90°.
- Un angle aigu est plus « petit » qu’un angle droit. Sa mesure sur le rapporteur est entre 0° et 90°.
- Un angle obtus est plus « grand » qu’un angle droit. Sa mesure sur le rapporteur est entre 90° et 180°.
- Un angle plat est formé de 2 demi-droites ayant des directions opposées. Sa mesure sur le rapporteur est 180°.
IV. Constructions
Construisons un angle de mesure . Nous allons le nommer .
- on commence par tracer une des demi-droite. Par exemple, ;

- on place le centre du rapporteur sur le sommet de l'angle, ici . Le côté du rapporteur doit être collé à la demi-droite tracée précédemment ;
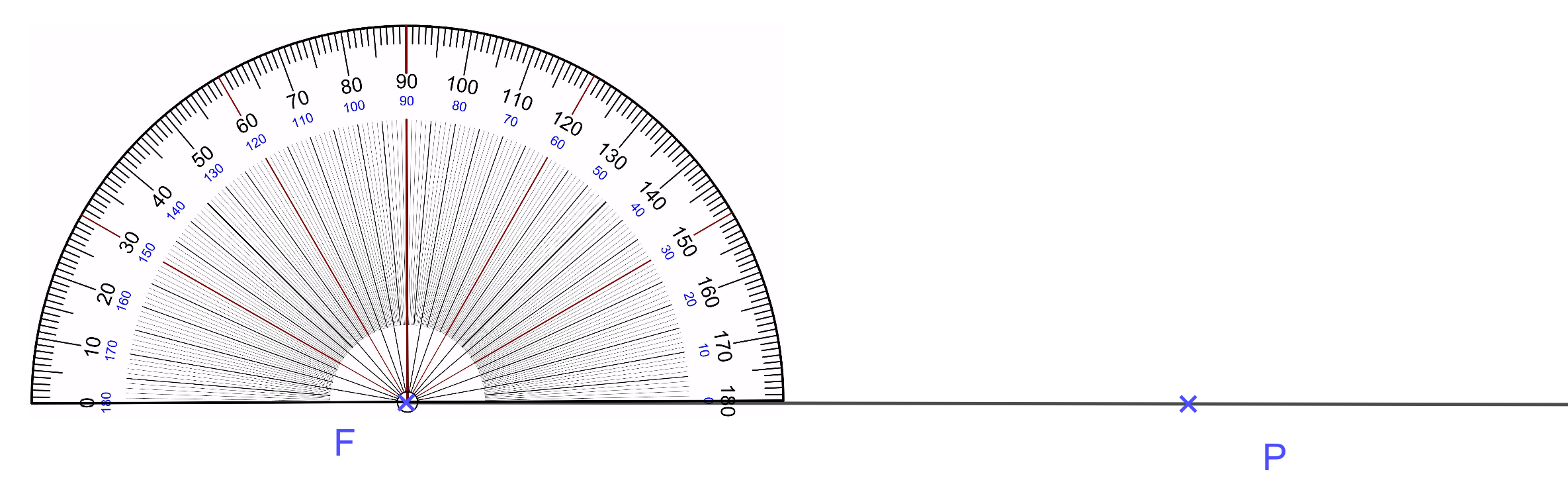
- on inscrit un point à la mesure souhaitée, ici .
Attention :
Si le rapporteur comporte deux 0, tu dois commencer par le 0 qui "touche" la demi-droite. Ici, c'est celui de droite.
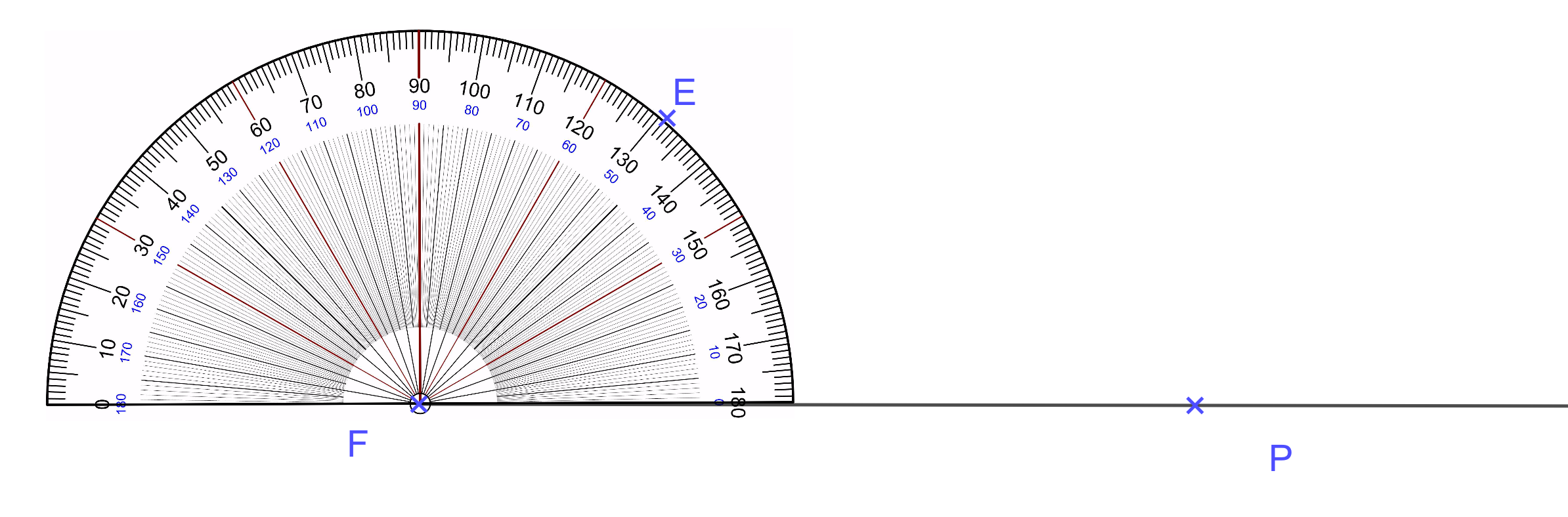
- on enlève le rapporteur et on trace la demi-droite ;
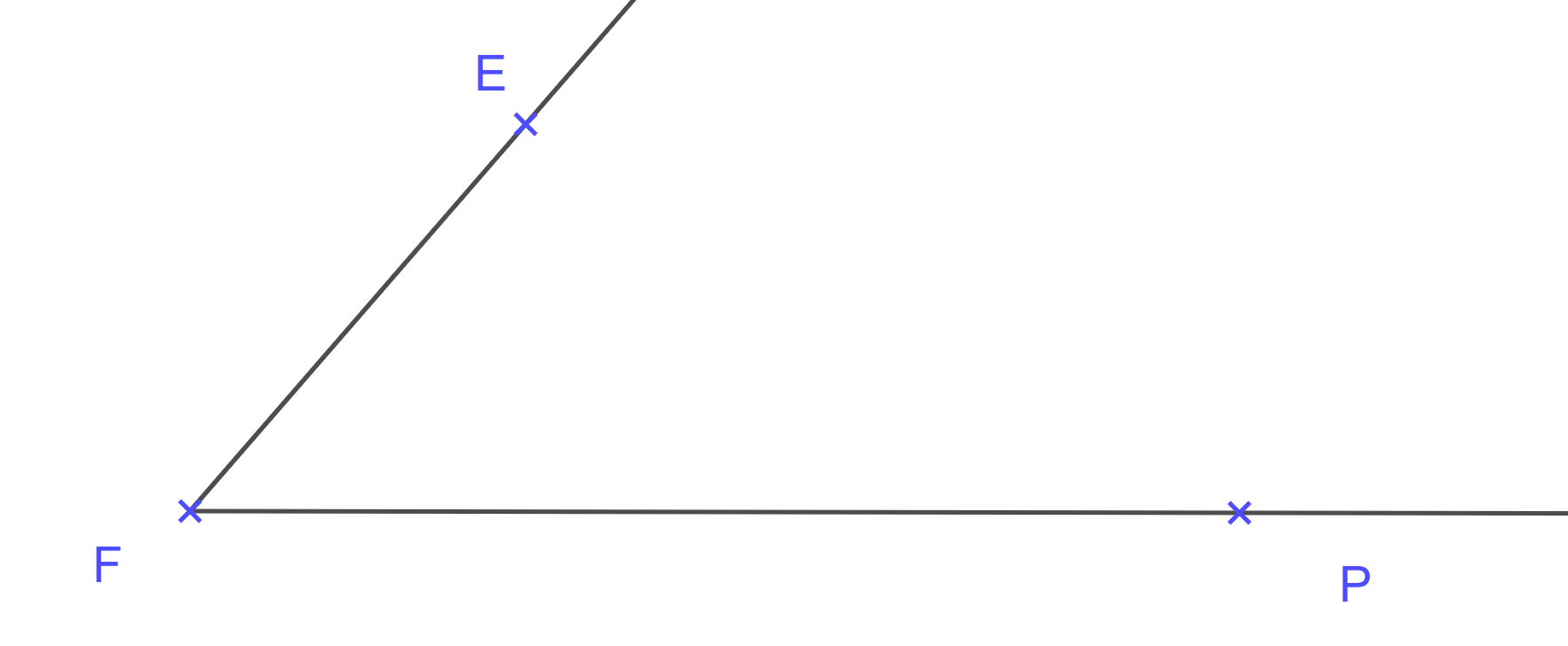
- on marque l'angle d'un arc de cercle et on inscrit sa mesure.