Les objets de la géométrie

I. Le point, la droite, le segment

1. Le point

Définition :
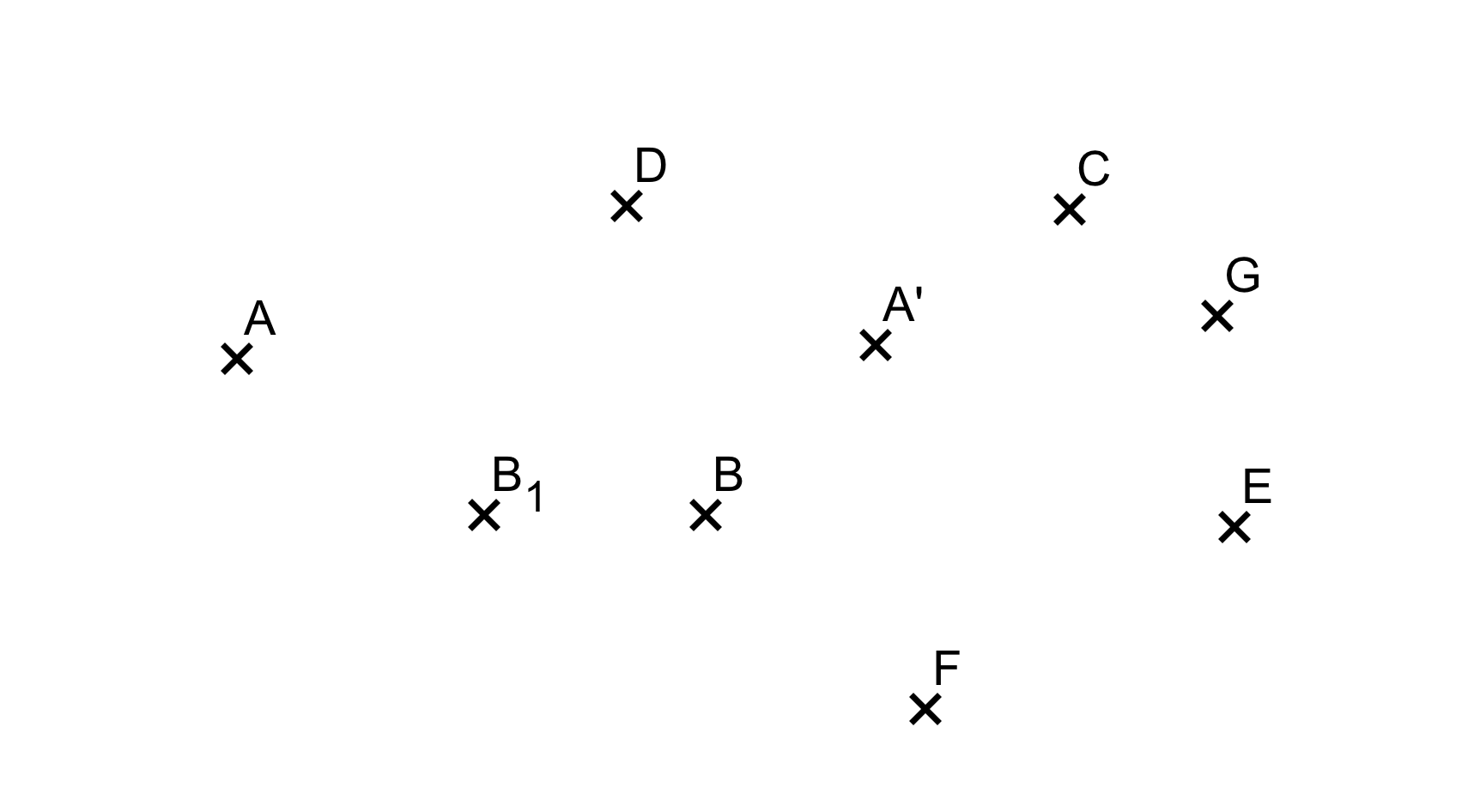
Un point est représenté par une croix, accompagné d'une lettre en majuscule.

Remarque :

Le point se trouve à l'endroit de la croix et non de la lettre ;
Deux points ne peuvent pas avoir le même nom.

Figure :

2. La droite

Définition :
Une droite est une ligne illimitée.

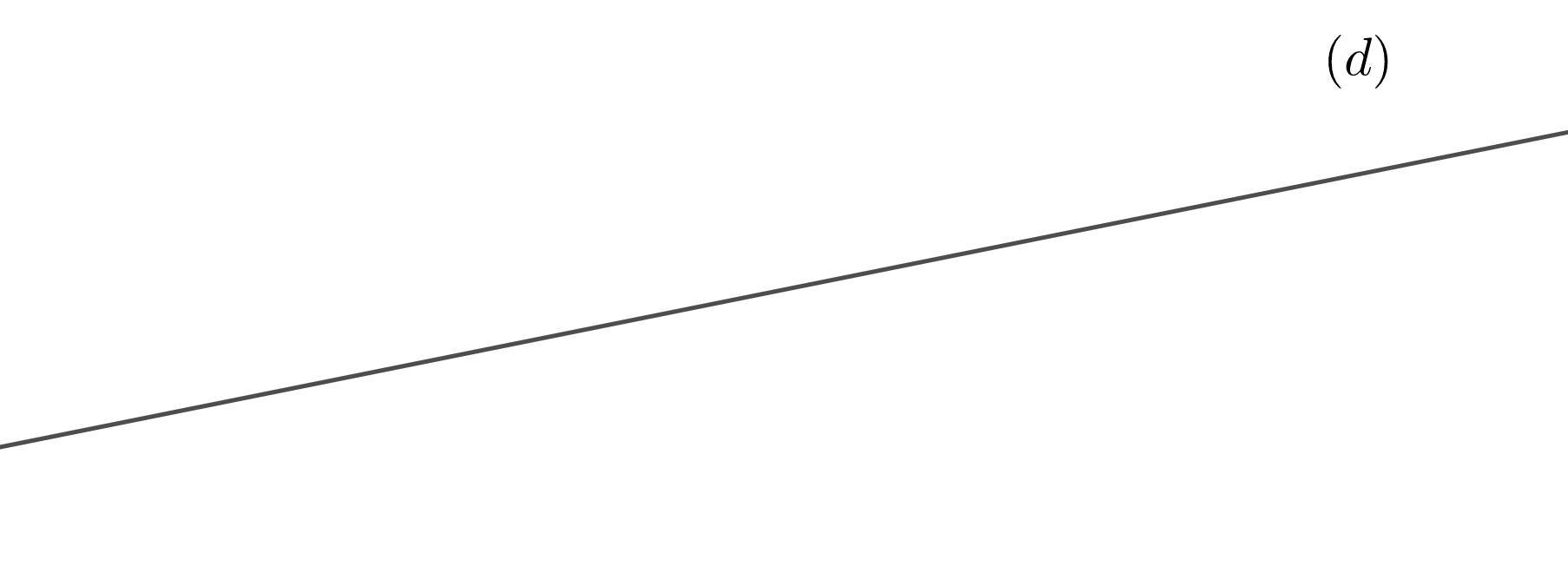
On a tracé une droite que l'on a nommée $(d)$ .

Propriété :
Par deux points distincts ne passe qu'une seule droite.

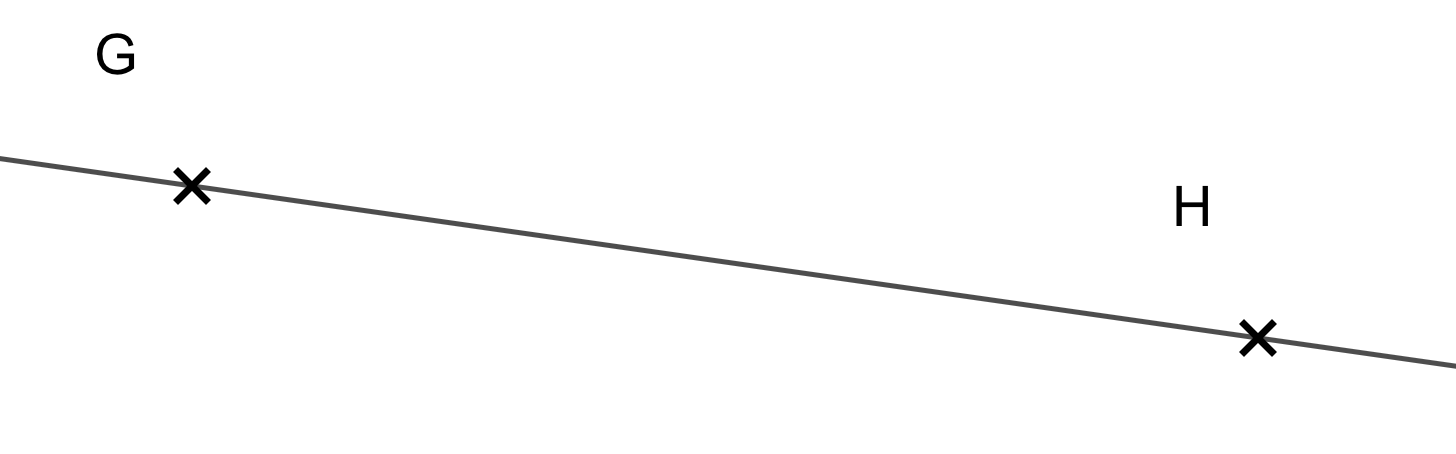
On peut nommer cette droite $(GH)$ ou $(HG)$ .

A l'écrit, on utilise la notation "entre parenthèses" pour préciser qu'il s'agit d'une droite.

3. Le segment

Définition :
Un segment est une portion de droite limitée par deux points, appelés extrémités.

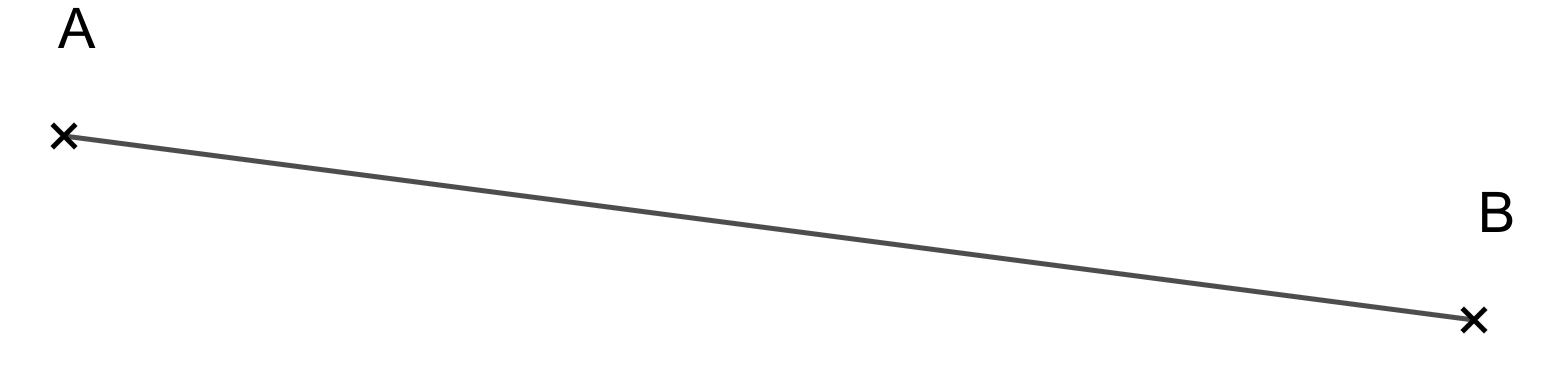
Ce segment a deux extrémités, on le note $[AB]$ ou $[BA]$ .
La longueur du segment $[AB]$ est notée $AB$ .

4. Milieu d'un segment

Définition :
Le milieu d'un segment est un point du segment qui le partage en deux segments de même longueur.

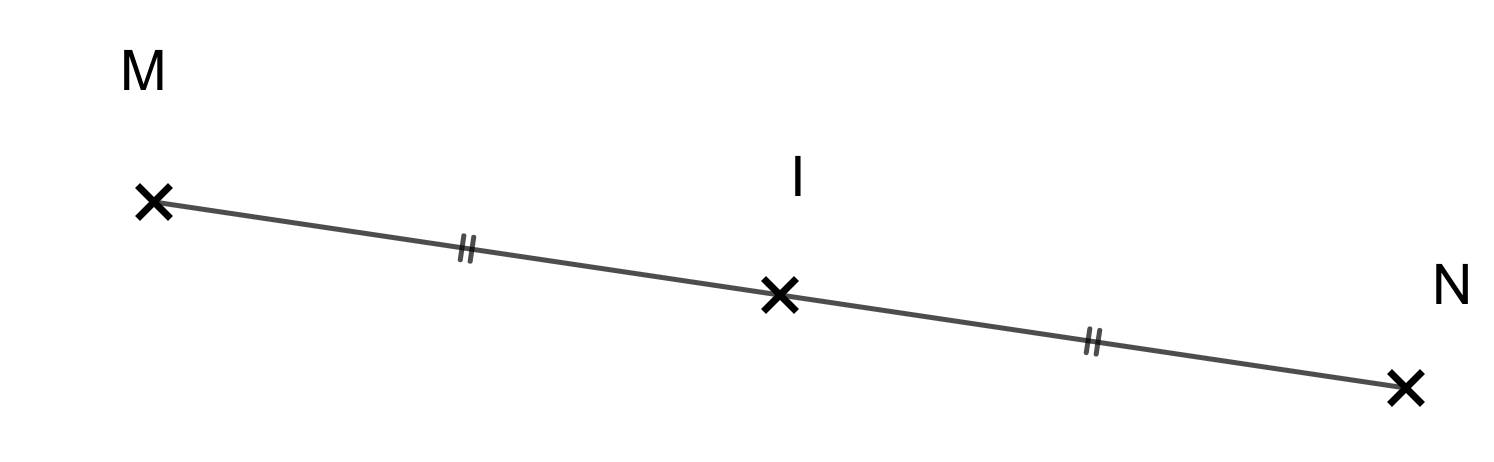
$I$ est le milieu du segment $[MN]$ .

Remarque :

On doit toujours coder la figure ;
Notation : " $I\in [MN]$ " veut dire " $I$ appartient au segment $[MN]$ .

$\in \textrm{veut dire "appartient à"}$

$\notin \textrm{veut dire "n'appartient pas à"}$

II. Le cercle

Définition :
Le cercle est un ensemble de points situé à une distance donnée d'un autre point appelé centre du cercle.
La distance donnée s'appelle rayon du cercle.

Exemple :
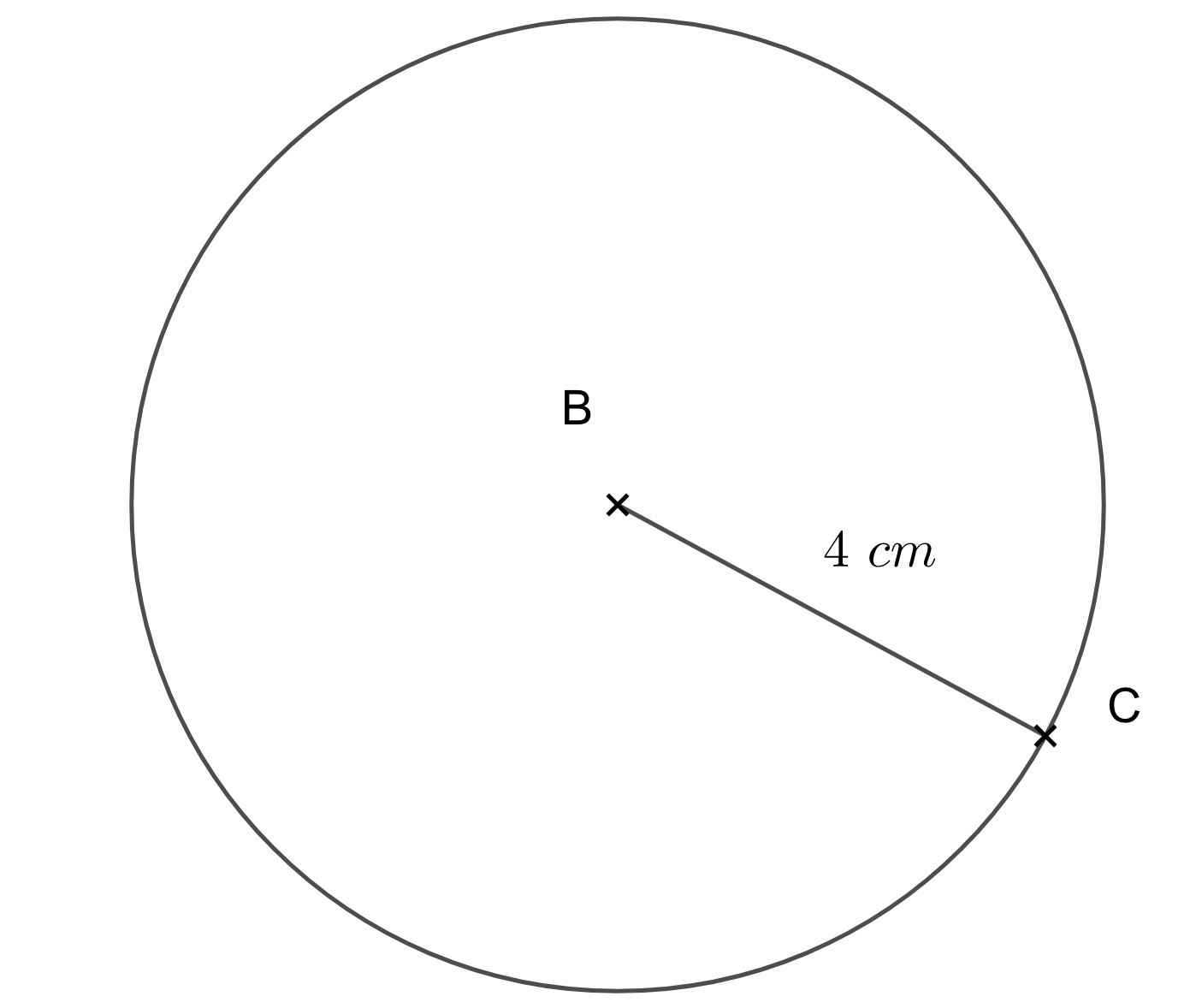
Pour tracer un cercle, on utilise un compas.

Ici

le centre du cercle est $B$ ;

le rayon du cercle est $4\ cm$ .

Définition :

Une corde est un segment reliant deux points du cercle.
Un diamètre est une corde passant par le centre du cercle.
Un arc de cercle est une portion du cercle situé entre deux points du cercle.
Un disque est l'ensemble des points à une distance du centre inférieure au rayon.

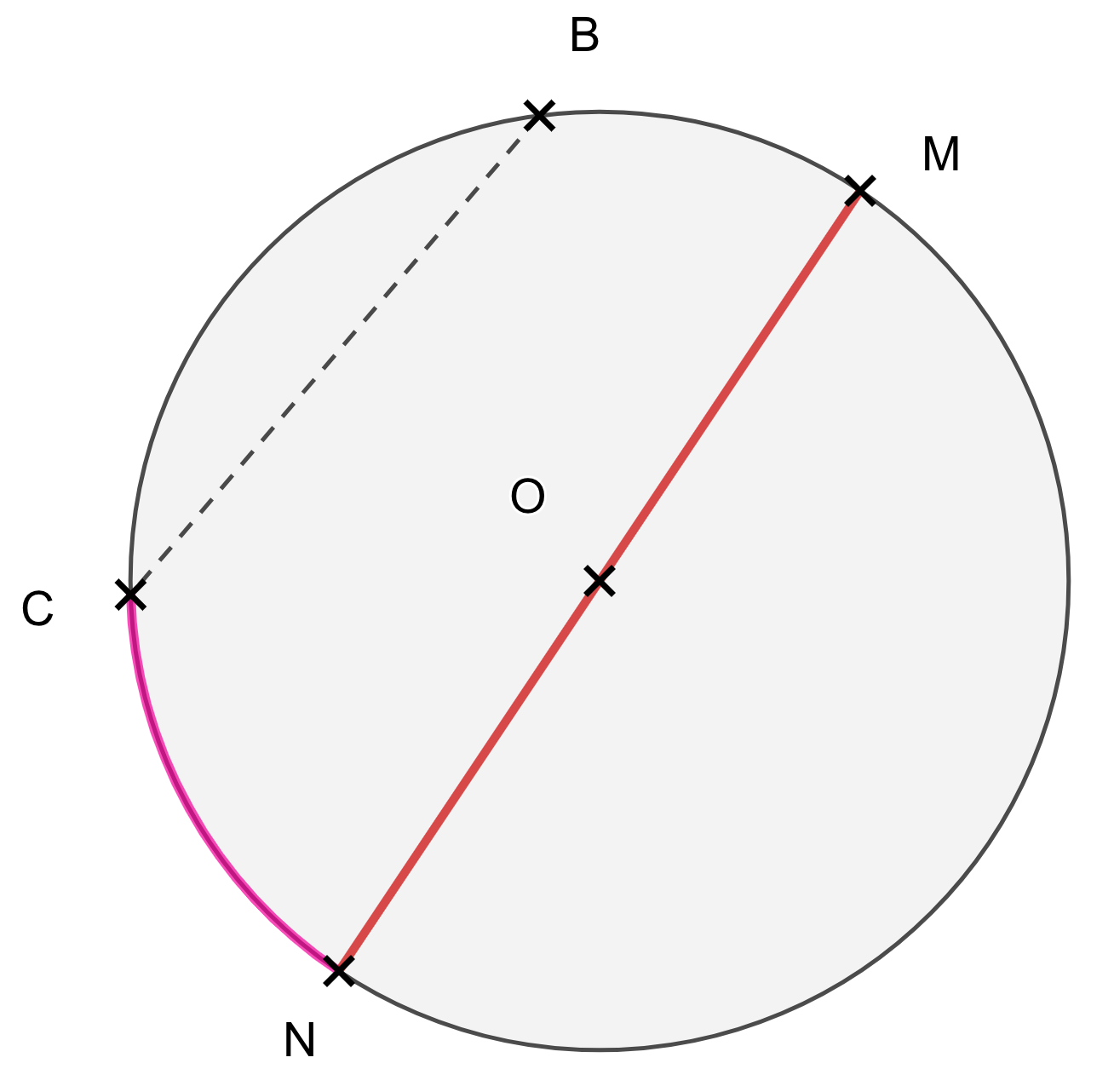
$[BC]$ (en pointillés) est une corde ;

$[MN]$ (en rouge) est un diamètre ;

$\overset{\huge{\frown}}{AB\:}$ (en rose) est un arc de cercle ;

En gris, il s'agit du disque.

III. Polygone

Définition :
Un polygone est une ligne brisée fermée.
C'est un figure composée de segments appelés côtés.
Les extrémités de chaque segment sont appelés sommets.

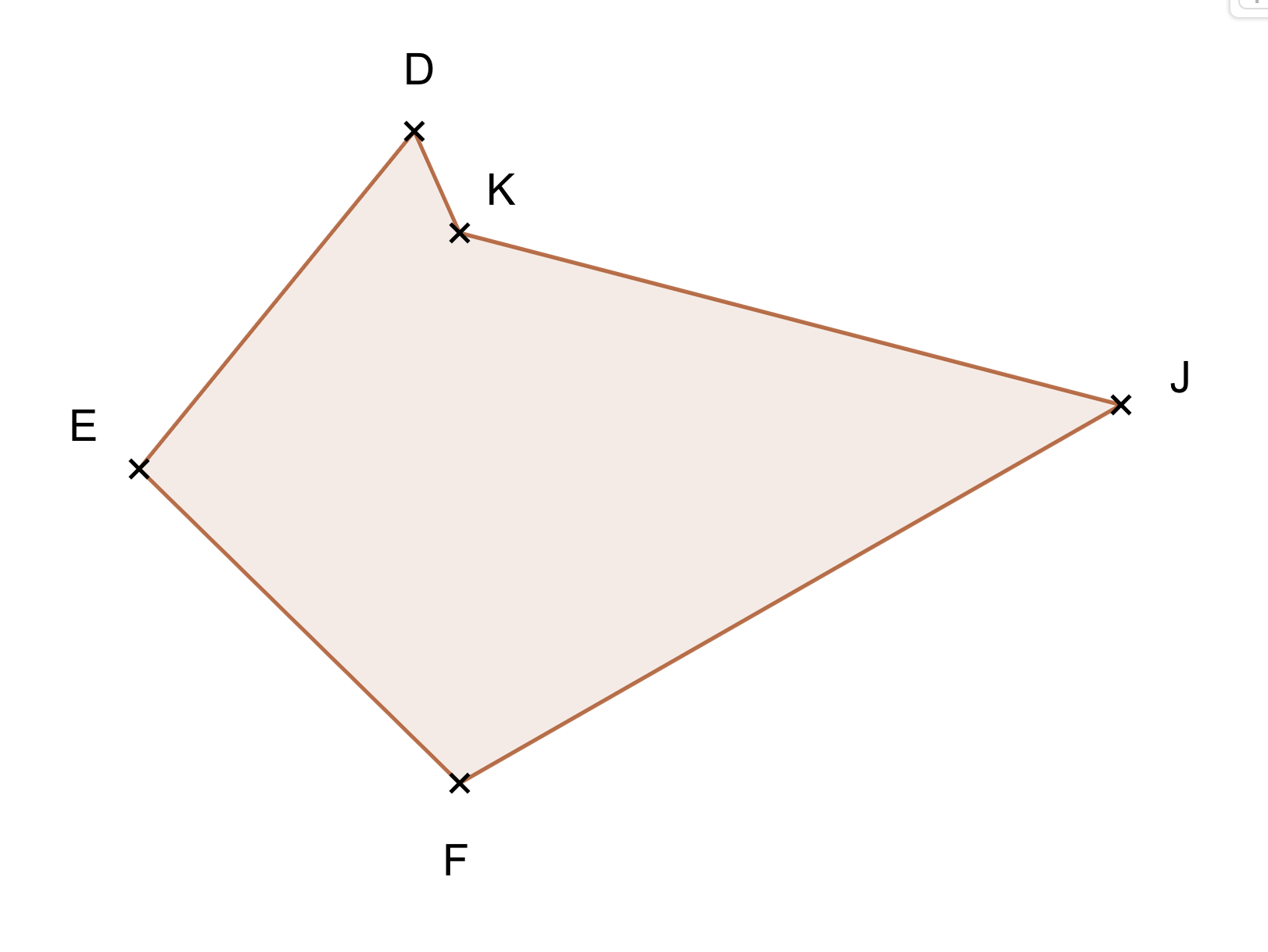
Exemple :

On a ici un polygone à cinq côtés. On peut le nommer $DEFJK$ .