Fractions

I. Partage de l'unité

Lorsqu’on partage une tarte en 4 parts égales, chaque part représente $\dfrac{1}{4}$ de la tarte et 3 parts représentent $3\times\dfrac{1}{4}$ de la tarte, qui s’écrit $\dfrac{3}{4}$.
On schématise la tarte par un disque et on colore en rouge les trois quarts.

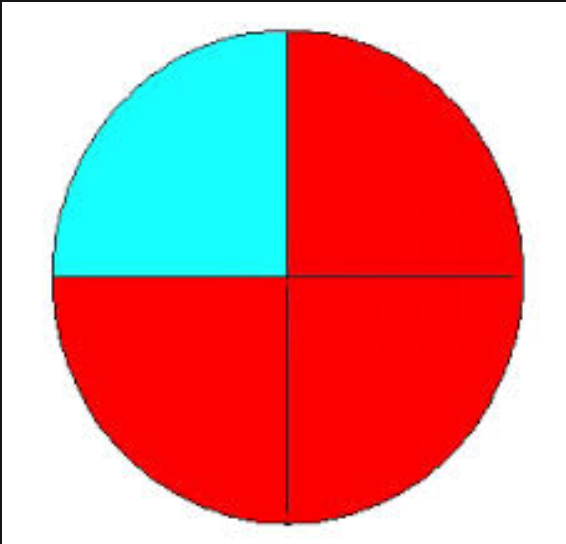
On peut aussi écrire que :

$\dfrac{3}{4}=\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}=3\times\dfrac{1}{4}$

Dans une unité, (ici, la tarte), il y a 4 parts (quarts). On a les égalités suivantes :

$\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}=4\times\dfrac{1}{4}=\dfrac{4}{4}=1$

II. Définition et vocabulaire

Exemple :
$\dfrac{2}{5}=2:5=0{,}4$. La division se termine, le nombre $\dfrac{2}{5}$ est un nombre décimal ;
$\dfrac{6}{11}=6:11\approx 0{,}55$. La division ne se termine pas, le nombre $\dfrac{6}{11}$ n'est pas un nombre décimal.

III. Demi-droite graduée

Exemple :
Placer les points suivants :

$A\left(\dfrac{6}{10}\right) ; B\left(\dfrac{3}{4}\right) ; C\left(\dfrac{2}{5}\right) ; D\left(\dfrac{3}{2}\right) ; E\left(\dfrac{8}{5}\right)$

Remarque :
Chaque graduation représente ici un dixième $\left(\dfrac{1}{10}\right)$. En effet, l'unité (entre le $0$ et le $1$) est partagée en $10$ parties, chaque partie représente donc un dixième $\left(\dfrac{1}{10}\right)$.

IV. Encadrement de nombre entiers

En utilisant une demi-droite graduée, on peut alors encadrer une fraction par deux nombres entiers consécutifs.

Exemple :
Sur la droite précédente, on a alors :

$\dfrac{2}{5}<\dfrac{6}{10}<\dfrac{3}{4}<\dfrac{3}{2}<\dfrac{8}{5}$

V. Fractions égales

Exemple :

• $\dfrac{2}{5}$ et $\dfrac{8}{20}$ sont égales car on a multiplié par $4$ le numérateur ET le dénominateur de la fraction $\dfrac{2}{5}$.
  On peut alors écrire :

$\dfrac{2}{5}=\dfrac{2\times 4}{5\times 4}=\dfrac{8}{20}$

• $\dfrac{28}{49}$ et $\dfrac{4}{7}$ sont égales car on a divisé par $7$ le numérateur ET le dénominateur de la fraction $\dfrac{28}{49}$.
  On peut alors écrire :

$\dfrac{28}{49}=\dfrac{28:7}{49:7}=\dfrac{4}{7}$

VI. Multiplication par une fraction

Prendre $\dfrac{5}{4}$ de $20$, c’est multiplier $\dfrac{5}{4}$ par $20$.

Exemple :

$\dfrac{5}{4}\times 20=\dfrac{5\times 20}{4}=\dfrac{100}{4}=25$

Trois méthodes différentes :

Prendre $\dfrac{7}{3}$ de $51$.