Les nombres décimaux

Commençons d'abord par rappeler le tableau de numération.

I. Fractions décimales et nombres décimaux

1. Fractions décimales

Exemple :
$\dfrac{34}{100}$ est une fraction décimale. Elle se lit trente-quatre centièmes.

On peut ranger ce dernier nombre dans le tableau rappelé au début du cours :

2. Des fractions décimales aux nombres décimaux

Exemple :
$5+\dfrac{4}{10}+\dfrac{7}{100}$ est un nombre décimal.
Sa partie entière est 5, c'est un nombre entier.
Sa partie décimale est $\dfrac{4}{10}+\dfrac{7}{100}$

3. Ecriture décimale ("écriture à virgule")

Un nombre décimal peut aussi s’écrire à l’aide d’une écriture à virgule appelée écriture décimale.

Exemple :
Considérons un nombre décimal :

$203+\dfrac{4}{10}+\dfrac{5}{100}$

Si on utilise le tableau de numération, on obtient :

$203+\dfrac{4}{10}+\dfrac{5}{100}$ s'écrit alors $203{,}45$
On place la virgule entre le chiffre des unités et celui des dixièmes.

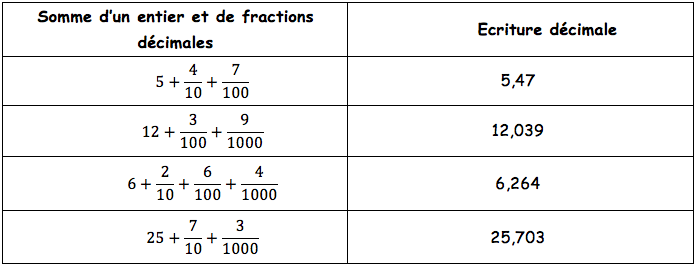
Voici quelques exemples :

4. Décomposer un nombre décimal

Reprenons le nombre $203+\dfrac{4}{10}+\dfrac{5}{100}$

$\begin{array}{ccc} 203{,}45&=&2\textrm{ centaines }+0\textrm{ dizaines }+3\textrm{ unités }+4\textrm{ dixièmes }+5\textrm{ centièmes}\\ &=&(2\times 100)+(0\times 10)+(3\times 1)+(4\times\dfrac{1}{10})+(5\times\dfrac{1}{100})\\ &=&(2\times 100)+(0\times 10)+(3\times 1)+(4\times 0{,}1)+(5\times 0{,}01) \end{array}$

II. Partie entière et partie décimale

Exemple :

Un nombre décimal est égal à la somme de sa partie entière et de sa partie décimale.

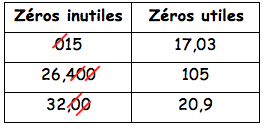
III. Les zéros inutiles

On peut ajouter ou supprimer des zéros à droite de la partir décimale ou à gauche de la partie entière sans changer le nombre.

Exemple :
Placer dans le tableau 015 – 26,400 - 17,03- 105 - 32,00 - 20,9

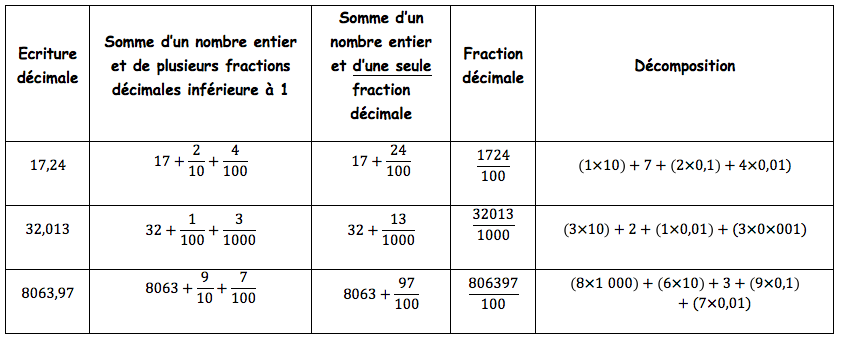
IV. Bilan : Les différentes écritures d’un nombre décimal