La fonction logartihme en terminale ES

I. Défintion et propriétés

1. Lien avec la fonction exponentielle

Chaque réel du demi axe des ordonnées est l'image d'un seul $x$ de l'axe des abscisses par la fonction exponentielle.

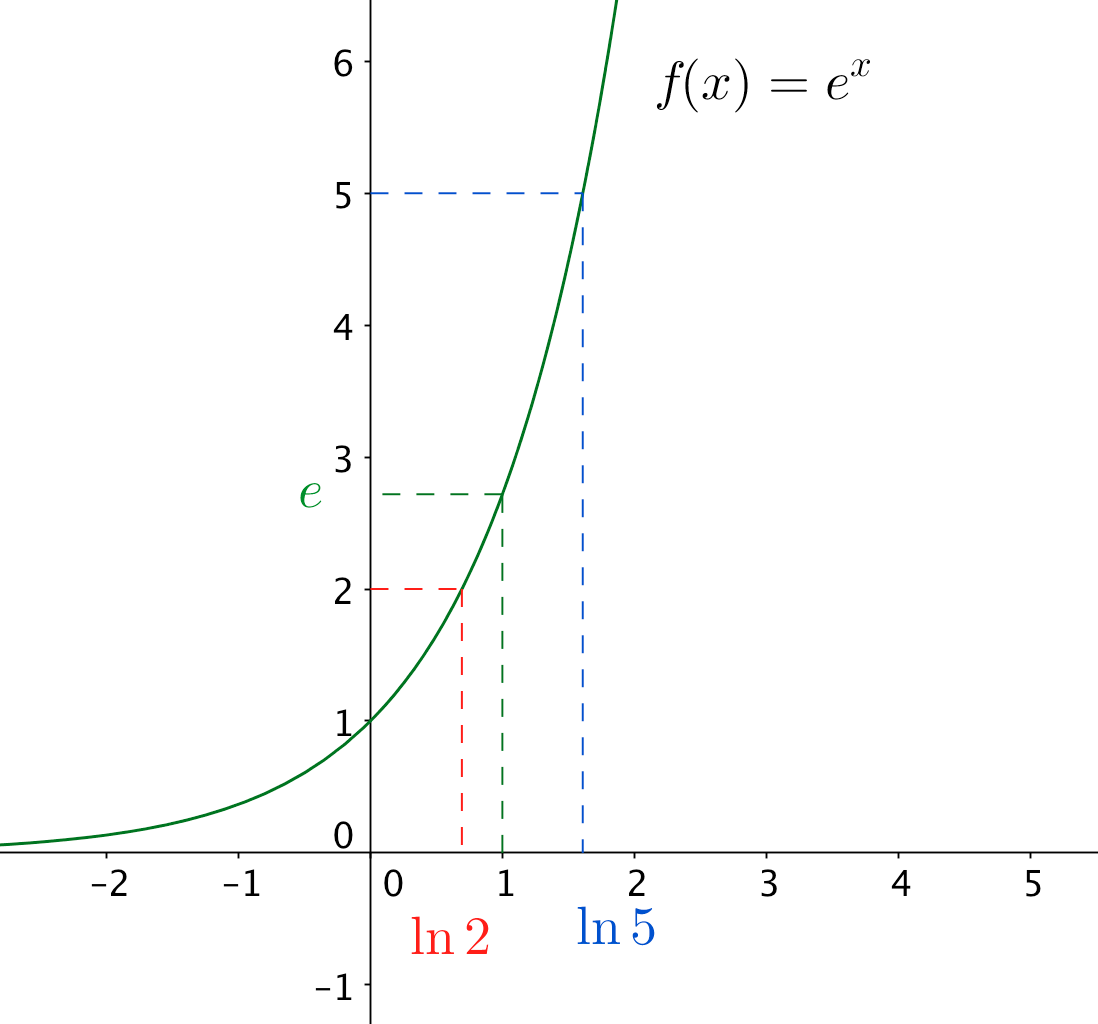
• $1$ est l'image de $0$ : $1=e^0$ ;
• $e$ est l'image de $1$ : $e=e^1$ ;
• $2$ est l'image du nombre noté $\ln 2$ : $e^{\ln 2}=2$ ;
• $5$ est l'image du nombre noté $\ln 5$ : $e^{\ln 5}=5$ .

On peut trouver des valeurs approchées à l'aide de la calculatrice :

$\ln 2\approx 0{,}693\textrm{ et }\ln 5=1{,}609$

2. Les conséquences

• $\ln a$ existe que si $a>0$ ;
• $\ln 1=0$ car $1=e^0$ ;
• $\ln e=1$ car $e=e^1$ ;
• Résolution d'équations :
  • $e^x=2\Longleftrightarrow x=\ln 2$ ;
  • $e^x=7\Longleftrightarrow x=\ln 7$ ;
  • $e^x=3{,}5\Longleftrightarrow x=\ln 3{,}5$ ;
  • $\ln x=2\Longleftrightarrow x=e^2$
  • $\ln x=-2,8\Longleftrightarrow x=e^{-2{,}8}$

On peut écrire alors la propriété suivante :

Conséquences immédiates :

• $e^{\ln a}=a,\ a>0$
• $\ln e^a=a$

3. Propriété du logarithme népérien

II. La fonction $\ln$ et les associées

1. La fonction $\ln$

On retrouve ici les premières propriétés de la fonction $\ln$.
On la définit par :

$\forall x\in\rbrack0;+\infty\lbrack,\ f(x)=\ln (x)=\ln x$

Sa dérivée est donnée par :

$(\ln x)'=\frac{1}{x}$

On dresse ici les variations de la fonction $\ln$ :
$\forall x\in\rbrack 0;+\infty\lbrack$, $\dfrac{1}{x}$ ne s'annule pas et reste toujours positif. Ainsi,

On en déduit que la fonction $\ln$ est strictement croissante.

On donne aussi quelques valeurs à connaître :

• $\ln e=1$
• $\ln 1=0$

Une primitive de $\dfrac{1}{x}$ est $\ln x$.
Il n'est pas nécessaire de connaître une primitive de $\ln x$, mais pour les curieux, $F(x)=x\ln x - x$ est un bon candidat !

2. Fonction $\ln u$

Si on considère que $g(x)=\ln (u(x))$, alors

$g'(x)=\frac{u'(x)}{u(x)}$

Exemple :
$g(x)=\ln (3x-4)$

$g'(x)=\frac{3}{3x-4}$

Une primitive de $\dfrac{u'}{u}$ est $\ln u$.

III. Fonction $\ln$ et équations "puissances"

Exemple :
Une action gagne 5% par an. Au bout de combien d'années aura-t-elle doublé ?
5% d'augmentation revient à mutliplier par $1{,}05$.
On cherche donc un entier $n$ représentant le nombre d'année tel que :

$p\times 1{,}05^n\geq 2\times p\textrm{ où }p\textrm{ est le prix d'une action.}$

$\begin{array}{ccc} 1{,}05^n & \geq & 2 \\ \ln (1{,}05^n) & \geq & \ln 2 \\ n\ln 1{,}05 & \geq & \ln 2 \\ n & \geq & \dfrac{\ln 2}{\ln 1{,}05} \end{array}$

$\dfrac{\ln 2}{\ln 1{,}05}\approx 14{,}21$
C'est donc au bout de 15 années que le prix de l'action aura doublé.