Lois de probabilités usuelles en Term ES

I. Lois discrètes

1. Loi de Bernoulli

Définition :
Une épreuve de Bernouilli est un expérience aléatoire qui a uniquement deux issues appelées Succès ou Echec.

Exemple :

On note $S$ l'évènement "avoir une bonne note". $\overline{S}$ est donc l'évènement avoir une mauvaise note.
Le succès a une probabilité notée $p$ et l'échec a donc une probabilité de $1-p$ .

On lance une pièce de monnaie. Si on considère que succès est "tomber sur Pile", il s'agit ici d'une épreuve de Bernoulli où la probabilité de "tomber sur pile" est $p$
( $\dfrac{1}{2}$ si la pièce est équilibrée)

On appelle cette expérience un épreuve de Bernoulli de paramètre $p$ .

2. Loi binomiale

Définition :
On répète $N$ fois une épreuve de Bernoulli de paramètre $p$ . Les épreuves sont indépendantes les unes des autres. On définit une variable aléatoire $X$ qui compte le nombre de succès.
$X$ suit alors une loi binomiale de paramètre $N$ et $p$ .

On note :

$X\hookrightarrow \mathcal B (N,p)$

Définition :
Le coefficient binomial $k$ parmi $n$ , noté $\dbinom{n}{k}$ , permet de déterminer les possibilités d'avoir $k$ succès parmi $n$ épreuves.

On peut calculer les coefficients binomiaux grâce à la formule suivante :

$\binom{n}{k}=\dfrac{n!}{k!(n-k)!}$

Propriété :

Soit $X$ une variable aléatoire suivant une loi binomiale de paramètre $n$ et $p$ . Sa loi de probabilité est donnée par la formule suivante :

$P(X=k)=\binom{n}{k}\times p^k\times (1-p)^{n-k}$

L'espérence mathématique est donnée par :

$E(X)=n\times p$

3. Exercice d'application

On lance un dé cubique ( $6$ faces) et équilibré et on note le chiffre apparu.
Combien faut-il de lancers pour obtenir au moins un $6$ avec une probabiltié de $0{,}99$ ?

Soit $X$ la variable aléatoire comptant le nombre de succès.
On considère qu'un succès est "obtenir $6$ "
$X$ suit alors une loi binomiale de paramètres $n$ et $p=\dfrac{1}{6}$ .

$\begin{array}{ccc} P(X\geq 1) &=& 1-P(X=0)\\ &=& 1-\dbinom{n}{0}\times \left( \dfrac{1}{6}\right) ^0\times \left( 1-\dfrac{1}{6}\right) ^n\\ &=& 1-1\times 1\times \left(\dfrac{5}{6}\right)^n\\ &=&1-\left(\dfrac{5}{6}\right)^n\\ \end{array}$

Ainsi, pour répondre à la question, on doit résoudre l'inéquation $P(X\geq 1)>0{,}99$

$\begin{array}{ccc} P(X\geq 1) &>& 0{,}99\\ 1-\left(\dfrac{5}{6}\right)^n &>& 0{,}99\\ -\left(\dfrac{5}{6}\right)^n &>& 0{,}99-1\\ \left(\dfrac{5}{6}\right)^n &<& 0{,}01\\ \ln\left(\dfrac{5}{6}\right)^n &<& \ln (0{,}01)\\ n\times\ln\left(\dfrac{5}{6}\right) &<& \ln (0{,}01)\\ n &>& \dfrac{\ln (0{,}01)}{-0{,}18} \end{array}$

En calculant à la calculatrice, on trouve environ $25{,}26$ , soit $26$ .

Il faut alors $26$ lancers du dé pour être sûr à $99\%$ d'obtenir au moins un $6$ .

II. Lois à densité

1. Généralités — Exercice d'approche

Il existe des variables aléatoires pouvant prendre théoriquement des valeurs dans un intervalle, on les appelle variables aléatoires continues.

Exemple :
Soit $X$ la variable aléatoire qui à un téléphone associe sa durée de vie en heures.
Considérons alors : $X\in\lbrack 0\ ;\ 25\ 000\rbrack$ , autrement dit, $X$ peut prendre toutes les valeurs entre $0$ et $25\ 000$ .
On déterminera alors les probabilités de la forme $P(X\le 10\ 000)$ ou $P(0\le X\le 15\ 000)$ . A l'aide d'une fonction donnée, ces probabilités seront égales à des aires.

Définition :
On appelle fonction de densité ou densité sur $\lbrack a\ ;\ b\rbrack$ toute fonction définie et positive sur $\lbrack a\ ;\ b\rbrack$ telle que

$\int_a^b f(x)\ dx=1$

Propriété :
Soit $X$ une variable aléatoire à valeurs dans $\lbrack a\ ;\ b\rbrack$ et une densité sur $\lbrack a\ ;\ b\rbrack$ .
On dit que $X$ suit une loi de densité $f$ si pour tous réels $c$ et $d$ appartenant à $\lbrack a\ ;\ b\rbrack$ , on a:

$\begin{array}{ccc} P(a\le X\le b)&=&1\\ P(c\le X\le d)&=&\int_c^d f(x)\ dx\\ P(X=c)&=&0\\ P(c\le X\le b)&=&1-P(a\le X\le c)\\ &=&1-\int_a^c f(x)\ dx\\ \end{array}$

2. Espérence

Propriété :
Soit $X$ une variable aléatoire continue sur $\lbrack a\ ;\ b\rbrack$ et $f$ sa fonction de densité sur $\lbrack a\ ;\ b\rbrack$ .
L'espérence mathématique de $X$ , notée $E(X)$ , est le réel défini par

$E(X)=\int_a^b xf(x)\ dx$

3. Loi uniforme

Définition :
Une variable aléatoire $X$ suit une loi uniforme sur $\lbrack a\ ;\ b\rbrack$ si elle admet comme densité la fonction $f$ définie sur $\lbrack a\ ;\ b\rbrack$ par

$f(x)=\frac{1}{b-a}$

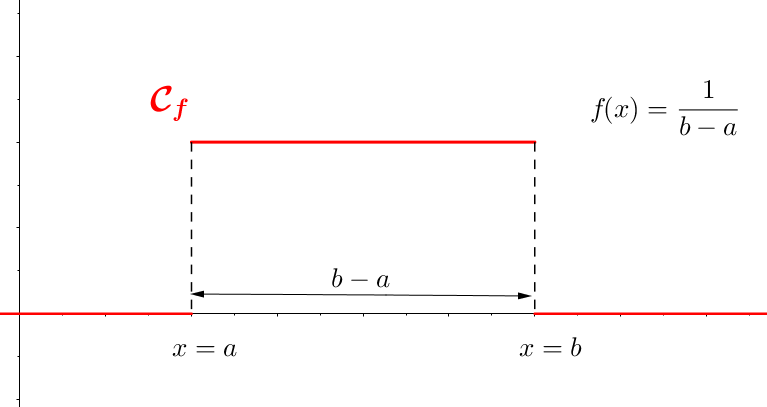
loi-uniforme

Propriété :
Soit $X$ une variable aléatoire suivant une loi uniforme sur $\lbrack a\ ;\ b\rbrack$ et $f$ sa densité.
A tout intervalle $\lbrack c\ ;\ d\rbrack\subset\lbrack a\ ;\ b\rbrack$ :

$P(c\le X\le d)=\dfrac{d-c}{b-a}$

Preuve :

$P(c\le X\le d)=\int_c^d f(x)\ dx=\int_c^d\dfrac{1}{b-a}\ dx=\left[\dfrac{1}{b-a}\right]_c^d = \dfrac{d-c}{b-a}$

Propriété :

$E(X)=\dfrac{a+b}{2}$

Preuve :

$\begin{array}{ccc} E(X)&=&\int_a^b xf(x)\ dx\\ &=&\int_a^b \dfrac{x}{b-a}\ dx\\ &=&\dfrac{1}{b-a}\int_a^b x\ dx\\ &=&\dfrac{1}{b-a}\left[\dfrac{x^2}{2}\right]_a^b\\ &=&\dfrac{1}{b-a}\left(\dfrac{b^2}{2}-\dfrac{a^2}{2}\right)\\ &=&\dfrac{1}{b-a}\dfrac{(b-a)(b+a)}{2}\\ &=&\dfrac{a+b}{2}\\ \end{array}$

4. Loi normale

a. La loi normale centrée réduite

Définition :
Une variable aléatoire $X$ de densité $f$ sur $\mathbb R$ suit une loi normale centrée réduite si

$f(x)=\dfrac{1}{\sqrt{2\pi}}\ e^{\frac{-x^2}{2}}$

On note cette loi : $\mathcal N(0,1)$
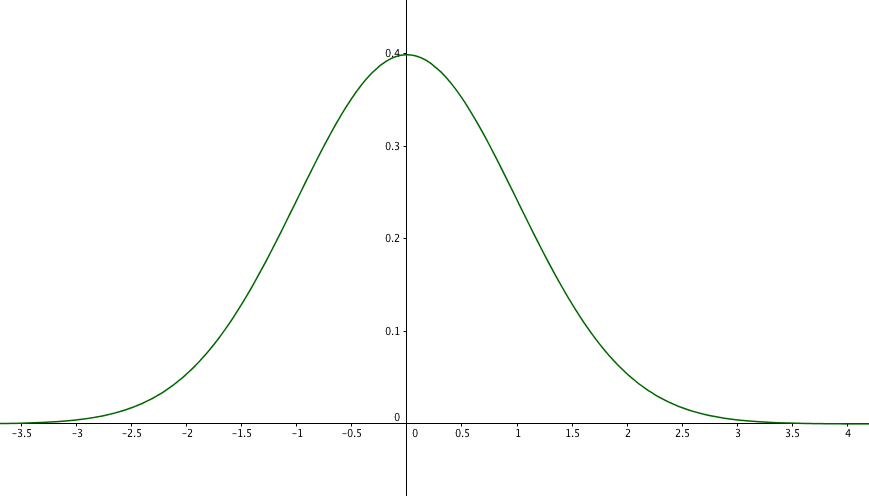
loi-normale-centree-reduite

Soit $\mathcal C_f$ sa représentation graphique.
On remarque que $\mathcal C_f$ est symétrique par rapport à l'axe des ordonnées.

Remarque :

L'espérence mathématique d'une loi normale centrée réduite est $0$ et l'écart type est $1$ .

D'après la définition d'une densité, on a :

$P(X\le a)=\int_{-\infty}^a f(x)\ dx$

La densité de la loi normale étant trop complexe à calculer, on utilisera la propriété suivante :

Propriété :
Soit $X$ une variable aléatoire suivant une loi normale centrée réduite.

$\begin{array}{ccc} P(X<0)&=&P(X\ge 0)&=&\dfrac{1}{2}\\ P(X\ge a)&=&1-P(X>a)\\ P(X\ge a)&=&0{,}5-P(0\le X\le a)&=&P(X\le -a)\\ P(-a\le X\le a)&=&1-2P(X\le a)\\ \end{array}$

Remarque :

Les probabilités pour les lois normales seront calculées à l'aide de la calculatrice.

Il peut être intéressant de retenir certaines valeurs usuelles.

b. Loi normale

Définition :
Soit $\mu$ un nombre réel et $\sigma$ un nombre réel strictement positif.
La variable aléatoire $X$ suit une loi normale, notée $\mathcal (\mu\ ;\sigma^2)$ si la variable aléatoire $Y$ définie par $Y=\dfrac{X-\mu}{\sigma^2}$ suit une loi normale centrée réduite $\mathcal N(0\ ;1)$

Propriété :
Soit $X$ une variable aléatoire suivant une loi normale $\mathcal N(\mu\ ;\sigma^2)$ . Alors l'espérence mathématique de $X$ est égale à $\mu$ et la variance de $X$ est égale à $\sigma^2$ .

On rappelle que la variance permet de mesurer la dispersion des valeurs autour de l'espérence.

On donne dans le graphique ci-dessus la représentation graphique pour une loi normale centrée réduite en vert, et en rouge, une loi normale quelconque où l'on peut changer les différentes valeurs de

\mu

\sigma

en faisant varier les curseurs.

On peut alors remarquer que plus la variance est élevée, plus les courbres sont "applaties".
Lorsque la variance est petite, l'aire sous la courbe est ressérée autour de l'espérence.

Propriété :
Soit $X$ une variable aléatoire suivant une loi normale $\mathcal N(\mu\ ;\sigma^2)$ .
On a les résultats suivants :

$P(\mu -\sigma\le X\le\mu +\sigma)\approx 0{,}68$
$P(\mu -2\sigma\le X\le\mu +2\sigma)\approx 0{,}95$
$P(\mu -3\sigma\le X\le\mu +3\sigma)\approx 0{,}99$

A l'aide de la calculatrice, on peut aussi déterminer un réel $a$ tel que $P(X\le a)=0{,}9$ .

Remarque :

L'expression $P(X\le a)=0{,}9$ revient à calculer l'aire de la partie hachurée. Cela revient donc au calcul d'une intégrale, qui peut s'avérer complexe.