La symétrie centrale en 5ème.

La symétrie centrale est une des premières transformations vue au collège. Le chapitre sur la symétrie centrale constitue un des piliers de la géométrie au collège. Il va être utile dans de nombreux chapitres, notamment concernant le parallélogramme.

I. Figures symétriques par rapport à un point.

Définition :
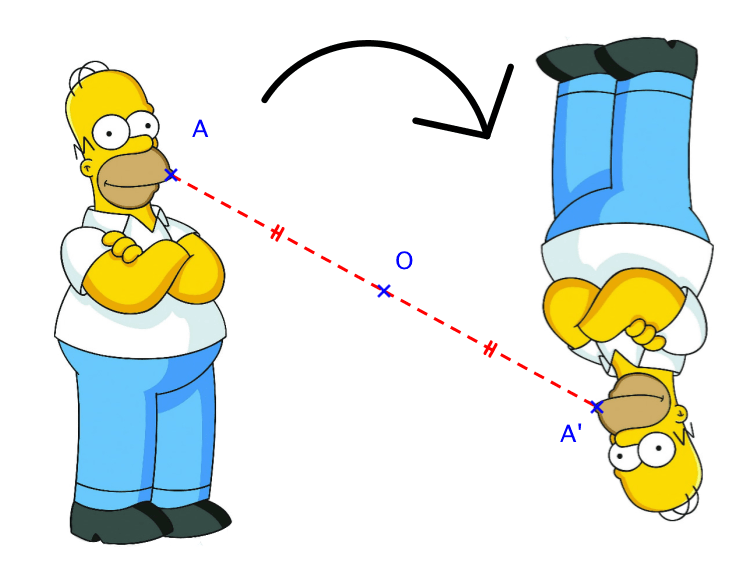
Deux figures sont dites symétriques par rapport à un point lorsqu'elles sont superposables par un demi-tour autour de ce point.

Exemple

Dans ce graphique les deux figures sont symétriques par rapport au point $O$ .
Pour tout point $A$ appartenant à la première figure, on cherche son symétrique $A'$ et l'on remarque qu'ils sont alignés avec $O$ et que : $AO=OA'$ .

Vocabulaire :
La symétrie par rapport à un point est aussi appelée symétrie centrale.

II. Propriétés de la symétrie centrale.

1. Symétrique d'un point.

Propriété :
Le symétrique d'un point $M$ par rapport à un point $O$ est le point $M$ vérifiant les propriétés suivantes :

$O$ , $M$ et $M'$ sont alignés ;
$O$ est le milieu de $[MM']$ .

Exemple :

$O$ est bien le milieu du segment $[MN]$ .

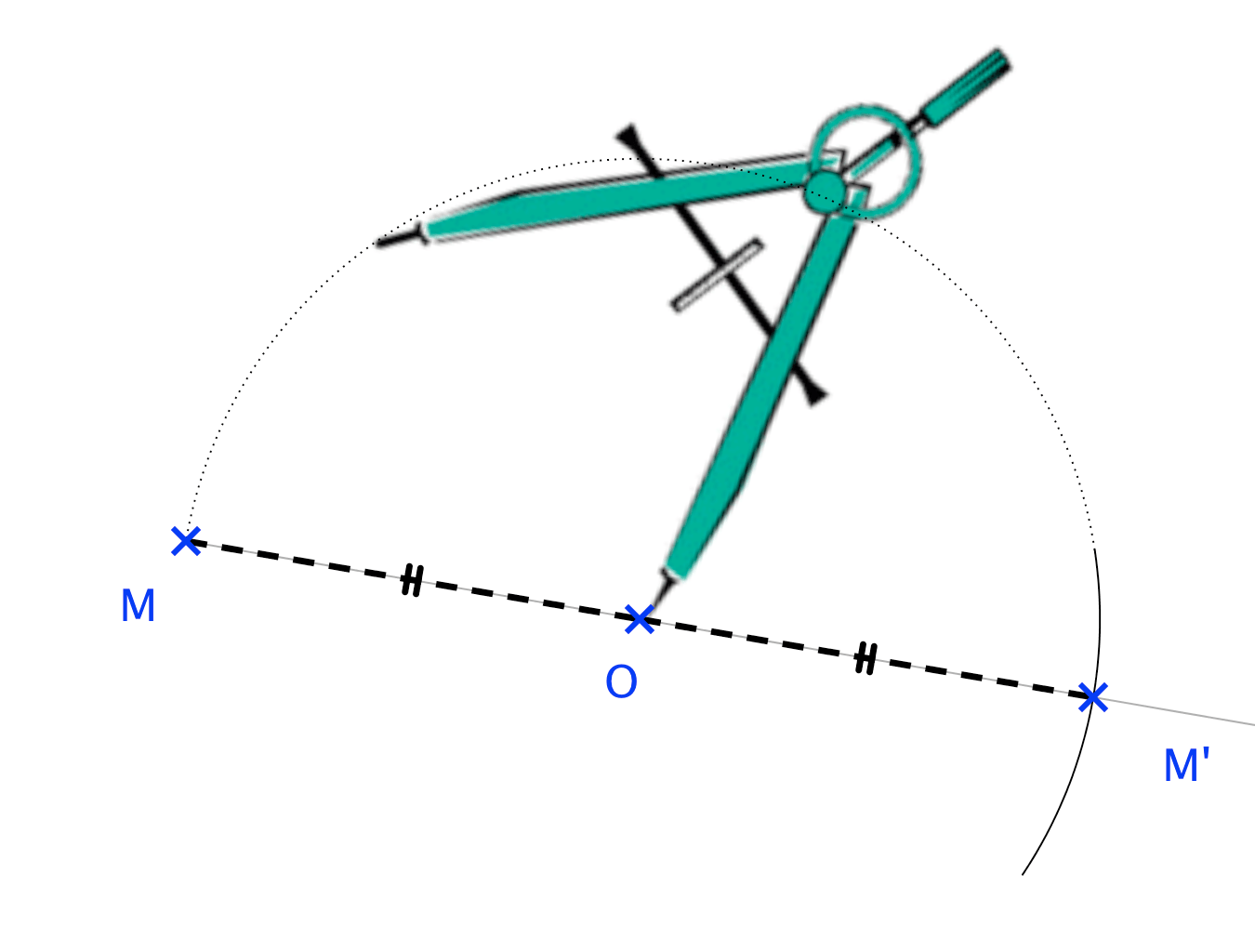
Procédé de construction :
Pour tracer le symétrique du point $M$ par rapport au point $O$ :

on commence par tracer la demi-droite $[MO)$ ] ;
on reporte ensuite la longueur $MO$ grâce au compas et on place ainsi le point $M'$ ;
on n'oublie pas de coder la figure et on laisse les traits de construction.

Remarque :
Ce procédé est très important : il est à la base de tout ce qui va suivre. S'il n'est pas acquis, il est nécessaire de l'approfondir en faisant plusieurs exercices.

2. Symétrique d'un segment.

Propriété :
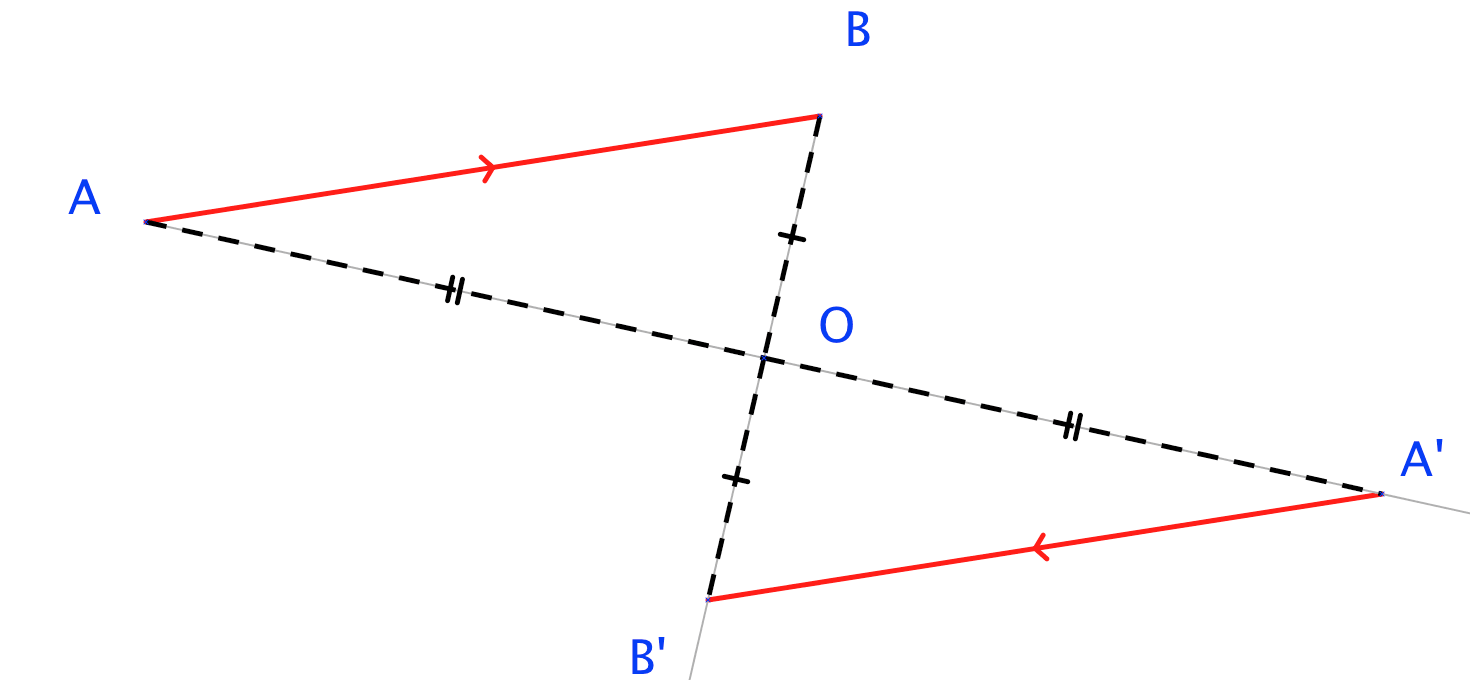
Le symétrique d'un segment par rapport à un point est un segment parallèle et de même longueur.

Exemple :

Procédé de construction :
Pour tracer le symétrique d'un segment $[AB]$ par rapport au point $O$ :

on trace les symétriques des points $A$ et $B$ par rapport à $O$ ;
on trace ensuite le segment $[A'B']$ ;
on n'oublie pas de coder la figure et on laisse les traits de construction.

3. Symétrique d'une droite.

Propriété :
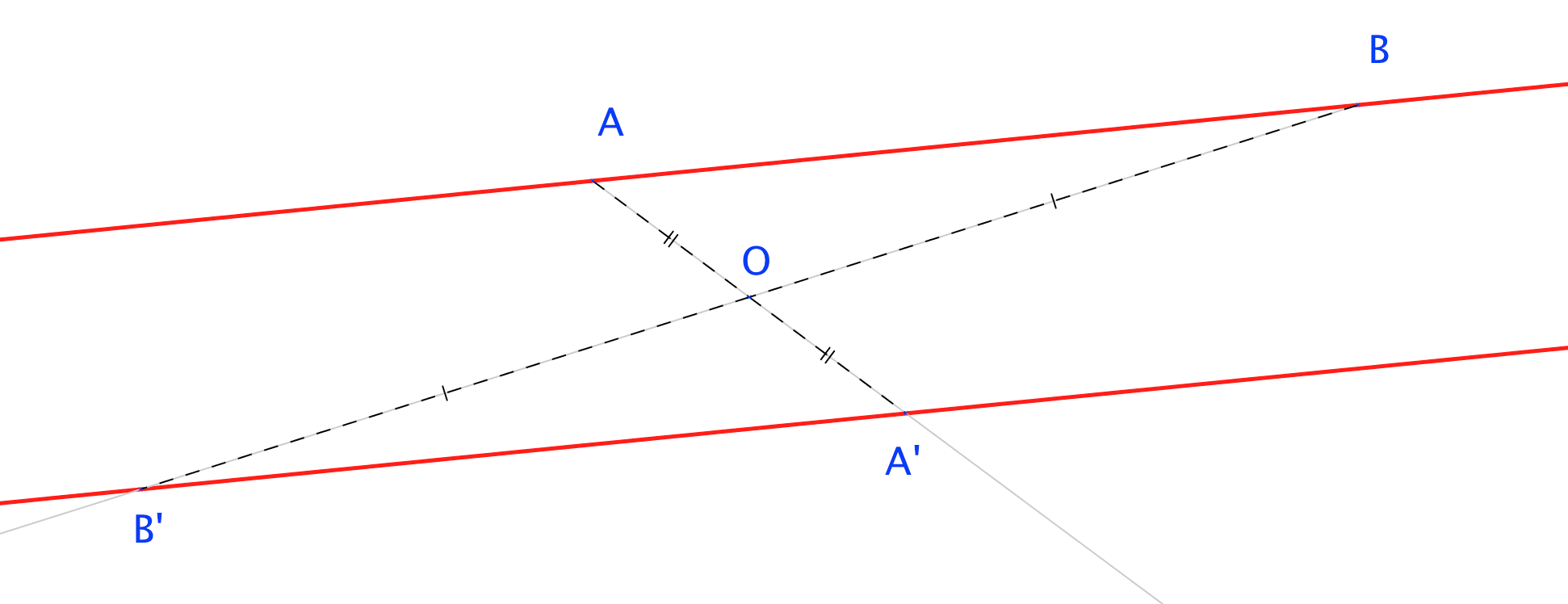
Le symétrique d'une droite par rapport à un point est une droite parallèle.

Exemple :

Procédé de construction :
Pour tracer le symétrique d'une droite $(AB)$ par rapport au point $O$ :

on trace les symétriques des points $A$ et $B$ par rapport à $O$ (s'ils n'apparaissent pas sur la droite, on peut en placer deux comme l'on veut) ;
on trace ensuite la droite $(A'B')$ ;
on n'oublie pas de coder la figure et on laisse les traits de construction.

4. Symétrique d'un cercle .

Propriété :
Le symétrique d'un cercle par rapport à un point est un cercle de même rayon.

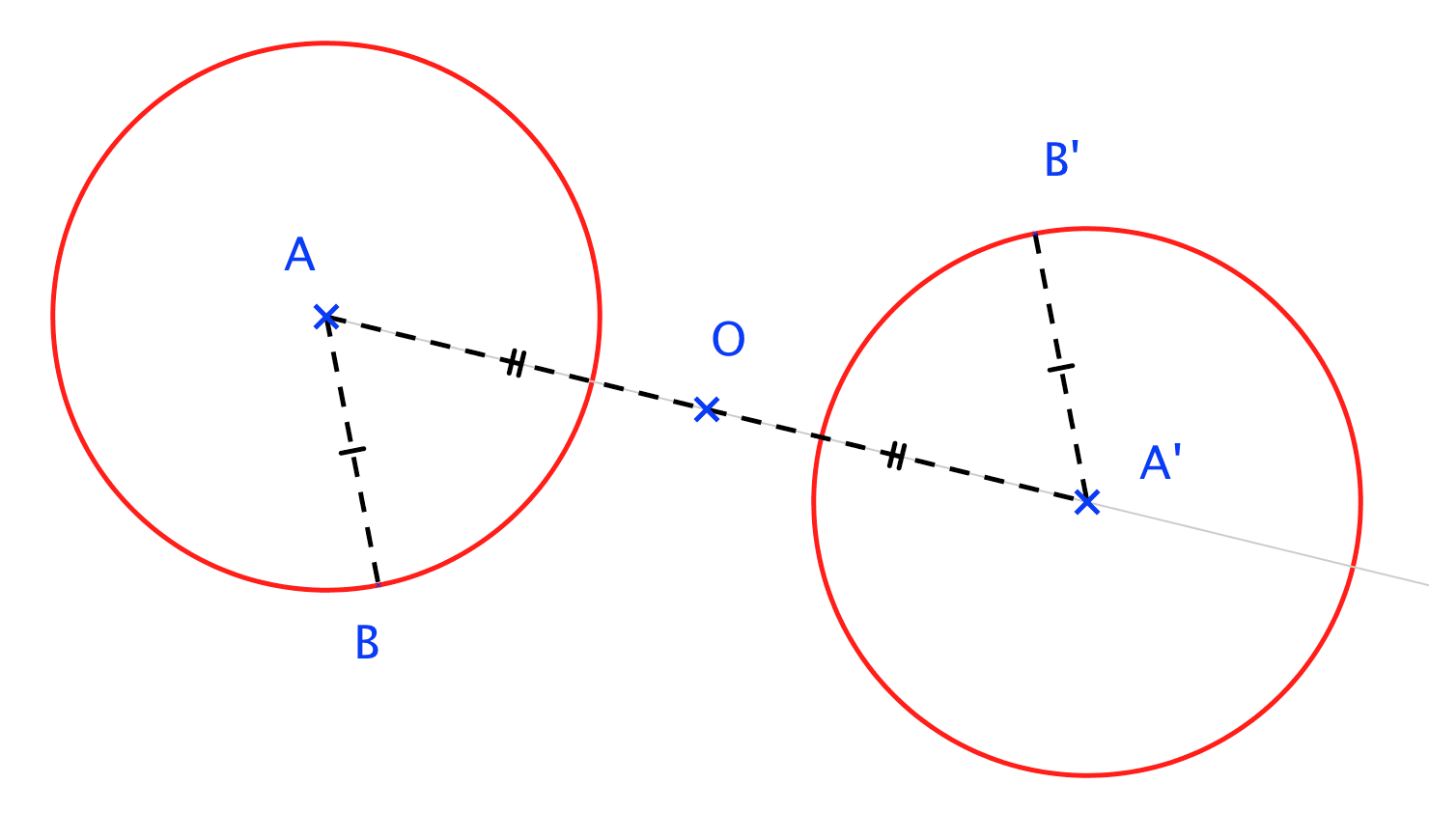
Exemple :

Procédé de construction :
Pour tracer le symétrique d'un cercle de centre $A$ par rapport au point $O$ :

on trace le symétrique du point $A$ par rapport à $O$ ;
on reporte le rayon du cercle en $A'$ et on trace le nouveau cercle ;
on n'oublie pas de coder la figure et on laisse les traits de construction.

III. Centre de symétrie.

Définition :
On dit qu'une figure admet un centre de symétrie si lorsque l'on effectue un demi-tour autour d'un point, on obtient deux figures superposables.
Ce point est appelé centre de symétrie

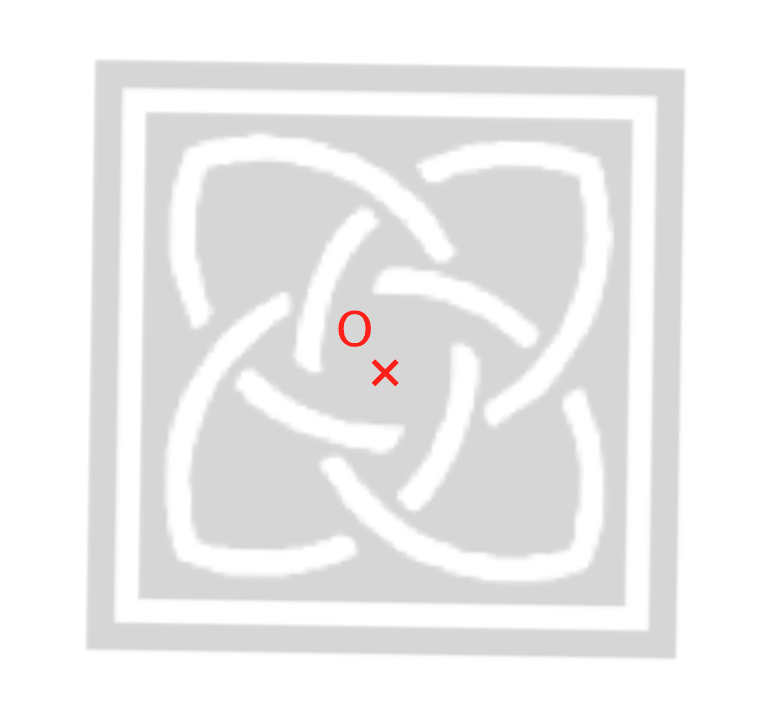
Exemple :

Cette figure admet un centre de symétrie.

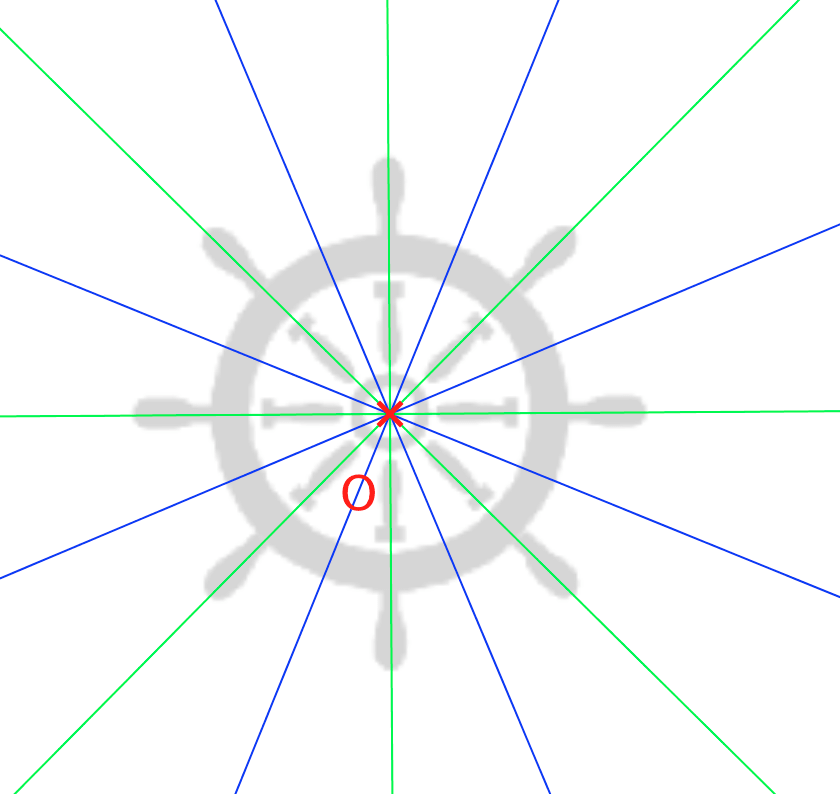
Cette figure admet un centre de symétrie et huit axes de symétrie.

La symétrie centrale en 5ème.

I. Figures symétriques par rapport à un point.

II. Propriétés de la symétrie centrale.

1. Symétrique d'un point.

2. Symétrique d'un segment.

3. Symétrique d'une droite.

4. Symétrique d'un cercle .

III. Centre de symétrie.

Toutes nos vidéos sur la symétrie centrale en 5ème

Posez vos questions

Fiches méthodes

Cours de mathématiques de cinquième