Les nombres décimaux en 5ème
I. Différentes écritures d'un nombre
Définition :
Un nombre décimal peut avoir plusieurs écritures :
- l'écriture décimale, à l'aide d'une virgule ;
- l'écriture fractionnaire, à l'aide d'une fraction ;
- à l'aide d'une décomposition en partie entière et partie décimale.
Exemple :
Le nombre quatre-vingt-trois virgule cent-quarante-sept peut s'écrire de plusieurs manières :
- est l'écriture décimale ;
- est l'écriture fractionnaire ;
- est la somme de sa partie entière et de sa partie décimale.
Remarque :
L'écriture permet de bien localiser le rang de chaque nombre. Ici, le chiffre des unités est 3, celui des dizaines est 8. Et le chiffre des dixièmes est 1, celui des centièmes est 4 et celui des millièmes est 7.
II. Comparer des nombres décimaux.
Règle :
Pour comparer des nombres décimaux, on commence par comparer les parties entières. On s'intéresse ensuite aux parties décimales : on compare les dixièmes, puis les centièmes, puis les millièmes, etc...
Exemple :
Comparons 81,719 et 81,72.
On remarque que les parties entières sont les mêmes.
Les chiffres des dixièmes sont égaux.
Pour les centièmes, 1 est inférieur à 2.
Ainsi, 81,72 est supérieur à 81,719
III. Demi-droite graduée.
Propriété :
Sur une demi-droite graduée :
- chaque point peut être repéré par un nombre, qu'on appelle abscisse du point ;
- à chaque nombre correspond un point.
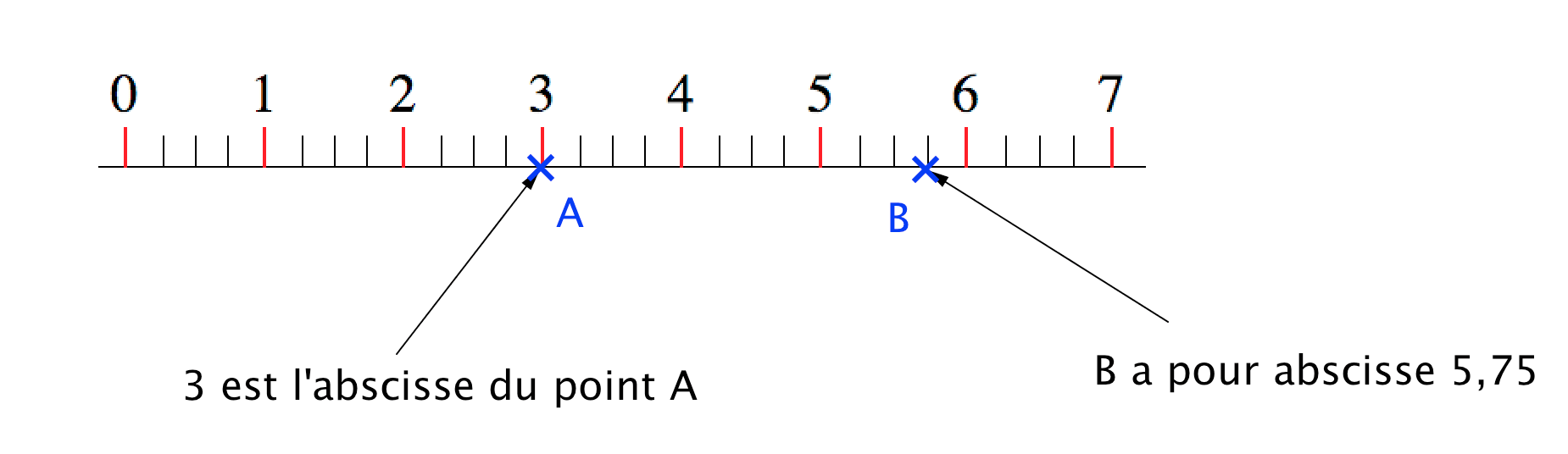
Exemple :
Toutes nos vidéos sur les nombres décimaux en 5ème