Calcul de l'aire ou surface d'un triangle rectangle

Vous devez calculer l'aire d'un triangle rectangle ?
Utilisez nos calculateurs gratuits et rapides pour un résultat immédiat ou pour vérifier les réponses de vos exercices.

Dans cette fiche-méthode, vous trouverez une courte introduction sur les propriétés du triangle rectangle, la formule générale pour calculer l'aire d'un triangle quelconque, la formule particulière du calcul de la surface d'un triangle rectangle et d'un triangle rectangle isocèle et des exercices.

Alors, comment faire pour calculer rapidement et facilement l'aire (également appelée surface) d'un triangle rectangle ?

Propriétés du triangle rectangle

Un triangle rectangle est un triangle dont l'un des angles est droit.

Un triangle rectangle est caractérisé par :

3 sommets et 3 côtés comme un triangle classique
1 angle droit
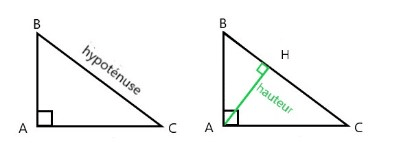
1 des côtés non adjacent à cet angle droit appelé hypothénuse
1 hauteur issue de l'angle droit du triangle notée $h$

Le triangle $ABC$ ci-dessous est rectangle en $A$ :
triangle_rectangle_en_A

Formule générale pour calculer l'aire d'un triangle quelconque

La formule généralement utilisée pour calculer l'aire (également appelée surface) d'un triangle quelconque :

$\boxed{A_{triangle}= \dfrac{b \times h}{2}}$

avec :

$A$ l'aire en $cm^2$
$b$ la base du triangle en cm
$h$ la hauteur du triangle en cm

Formule particulière calcul de l'aire d'un triangle rectangle

En multipliant les deux longueurs des côtés adjacents à l'angle droit

Cette formule s'applique au triangle rectangle en multipliant la longueur des deux côtés du triangle qui ne sont pas l'hypothénuse, ici $AB$ et $AC$ .

Pour calcul le triangle rectangle $ABC$ rectangle en $A$ , on applique donc la formule :

$\boxed{A_{trianglerectangle}= \dfrac{AC \times AB}{2}}$
avec :

$A$ en $cm^2$
$AC$ en cm
$AB$ en cm

Pour un triangle $ABC$ rectangle en A, avec $AB=3cm$ , $AC=4cm$ et $BC=5cm$ , le calcul de l'aire de ABC donne :

${A_{ABC}= \dfrac{AC \times AB}{2}}=\dfrac{ 4 \times 3}{2}= \dfrac{12}{2}=\boxed{6cm^2}$

Cas particulier du triangle rectangle isocèle :

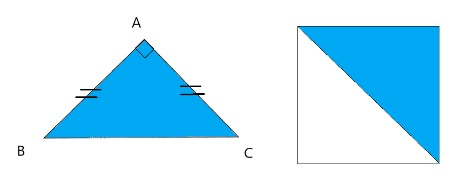
Dans le cas du triangle isocèle, $AB=AC$ , la formule utilisée pour calculer l'aire du triangle rectangle isocèle sera alors la suivante :

$\boxed{A_{trianglerectangleisocele}= \dfrac{AC \times AB}{2}= \dfrac{AB^2}{2}= \dfrac{AC^2}{2}}$
avec :

$A$ en $cm^2$
$AC$ en cm
$AB$ en cm

NB : sur l'illustration, on remarque que l'aire du triangle rectangle isocèle correspond à la moitié de la surface du carré (ou aire du carré).

Explication : lien entre aire du rectangle et surface du triangle rectangle

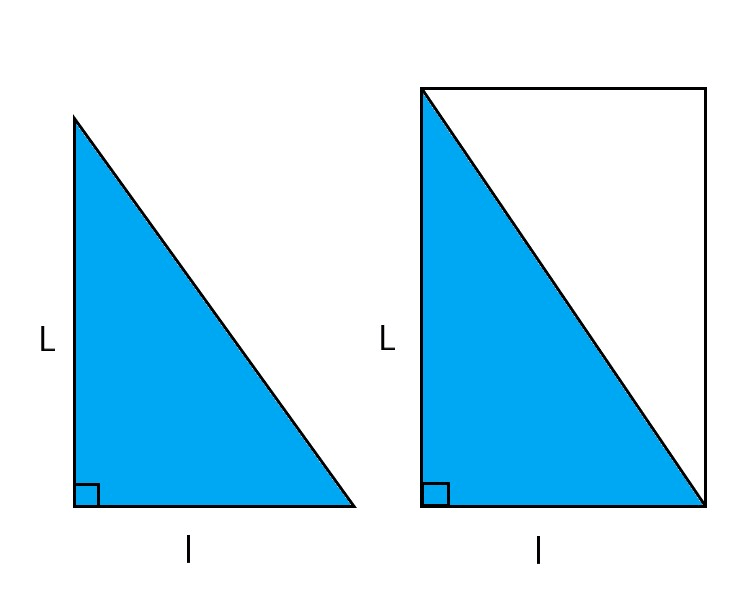
triangle_rectangle_aire

On voit bien sur l'illustration ci-dessus que l'aire du triangle rectangle (en bleu) représente la moitié de l'aire du rectangle aux mêmes dimensions (même longueur $L$ et même largeur $l$ ).

Or, on sait que pour calculer la surface d'un rectangle, en $cm^2$ , la formule à appliquer est la suivante :

$A_{rectangle}= l \times L$
avec :

$l$ la largeur du rectangle en $cm^2$
$L$ la longueur du rectangle en $cm^2$

Puisque l'aire du triangle rectangle correspond à la moitié de la surface du rectangle aux mêmes dimensions, on en déduit la formule pour calculer la surface du triangle rectangle :

$A_{trianglerectangle}= \dfrac{A_{rectangle}}{2} = \boxed{\dfrac{l \times L}{2} = \frac{b \times h}{2}}$
avec :

$l$ la base du triangle en $cm^2$ que l'on peut également noter $b$
$L$ la hauteur du triangle en $cm^2$ que l'on peut également noter $h$

Avec la longueur de la hauteur du triangle rectangle et l'hypothénuse

S'il vous manque la longueur d'un des côtés adjacents à l'angle droit du triangle rectangle dont vous devez calculer l'aire, vous pouvez opter pour la formule générale de calcul de l'aire d'un triangle.

Dans le cas d'un triangle rectangle, la base $b$ correspond à l'hypothénuse et la hauteur $h$ est toujours issue de l'angle droit comme sur le schéma qui suit.

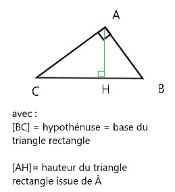
triangle_rectangle_hauteur_base

Ainsi, si vous avez la longueur de la base et de la hauteur de votre triangle rectangle, vous pouvez appliquer la formule suivante :

$\boxed{A_{trianglerectangle}= \dfrac{b \times h}{2}}$

avec :

$A$ l'aire en $cm^2$
$b$ la base du triangle rectangle ou longueur de l'hypothénuse en cm
$h$ la hauteur du triangle, issue de l'angle droit du triangle rectangle, en cm

Comment calculer la hauteur, l'hypothénuse ou la longueur d'un côté du triangle ?

Super ces formules ! Mais il vous manque une information qui n'est pas donnée dans l'énoncé ? Généralement, l'exercice vous amènera à calculer l'hypothénuse, la longueur d'un côté ou la hauteur du triangle rectangle.

Le théorème de Pythagore

Pour calculer la longueur d'un côté du triangle ou la longueur de l'hypothénuse, vous pourrez vous servir du triangle de Pythagore.

Rappel de énoncé du théorème de Pythagore pour le triangle $ABC$ rectangle en $A$ :

$BC^2=AC^2+BC^2$
avec :

$BC$ l'hypothénuse du triangle en $cm$
$AC$ et $BC$ les côtés adjacents à l'angle droit $\hat{A}$

Le théorème des cathètes

Si vous souhaitez calculer la hauteur $h$ du triangle $ABC$ rectangle en $\hat{A}$ , la formule à appliquer est la suivante :

$\boxed{h = \dfrac{AB \times AC}{BC}}$
avec :

BC la longueur de l'hypothénuse en cm
AB et AC la longueur des côtés adjacents à l'angle droit

Dans le cas de l'exemple précédent du triangle $ABC$ rectangle en A, avec $AB=3cm$ , $AC=4cm$ et $BC=5cm$ , la hauteur $AH$ est calculée comme suit :

$h = \dfrac{3 \times 4}{5}= \dfrac{12}{5}=\boxed{2{,}4cm}$

Si l'on applique la formule générale de calcul de l'aire avec la base et la hauteur du triangle, on trouve le même résultat que précédement.

$A_{ABC}= \dfrac{b \times h}{2}=\dfrac{5 \times 2{,}4}{2}=\dfrac{12}{2}=\boxed{6cm^2}$

Calculateurs gratuits d'aire de triangle rectangle

Cette fiche détaille toutes les modalités de calcul de l'aire d'un triangle rectangle ou surface du triangle rectangle.

Vous n'avez pas envie de faire les calculs vous-même ?
Ou vous voulez vérifier les résultats de vos exercices ou DM ?

Voici deux outils qui vous serviront à calculer automatiquement (et gratuitement) l'aire ou la surface d'un triangle rectangle et un partenaire de Mathforu qui pourrait avoir à utiliser le calcul de surface :)