Calculer le volume d'une sphère

Profitez de notre calculateur gratuit pour calculer le volume d'une sphère.

Alors, comment faire pour calculer rapidement et facilement le volume d'une sphère ?

Vous trouverez toutes les réponses à vos questions dans cette fiche-méthode.

• Quelle est la différence entre sphère et boule ?
• Comment calculer le volume d'une boule avec son rayon ou avec son diamètre ?
• Comment calculer le volume d'une demi-boule ou demi-sphère ?
• Comment calculer le volume d'une boule creuse ?
• Comment calculer le volume d'une sphère tronquée ou d'une calotte sphérique?

Propriétés d'une sphère

En géométrie, une sphère correspond à une surface.
Tous les points de la sphère sont situés à une même distance du centre.
La distance entre le centre $C$ et les points constituant la sphère correspond au rayon $r$ de la sphère.

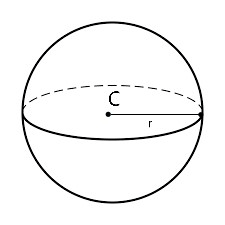
La sphère est généralement creuse, puisqu'elle correspond à une surface : elle n'a donc pas de volume à proprement parler. On calcule plutôt l'aire d'une sphère.

Mais alors à quoi se réfère t-on lorsque l'on se réfère au calcul du volume d'une sphère en mathématiques ? On parle en réalité du calcul du volume d'une boule, l'équivalent d'une sphère pleine.

Différence entre sphère et boule

La première différence entre boule et sphère est que la sphère correspond à une surface fermée tandis que la boule correspond à un solide de révolution qui n'est autre que délimité par une sphère.

Si vous vous imaginez le solide résultant de la rotation d'un disque autour de n'importe lequel de ses diamètres : c'est ce à quoi correspond la boule.

Quels sont les points qui appartiennent à la boule ?

Les points de la sphère ne correspondent qu'à ceux qui sont situés à la même distance du centre, soit le rayon $r$.

Quant aux points de la boule, puisque c'est un solide, ce sont tous ceux qui se trouvent à une distance inférieure ou égale à $r$ du centre.

Formule calcul du volume d'une sphère pleine ou boule

Il existe au moins 2 manières différentes de calculer le volume d'une sphère pleine ou boule : à l'aide du rayon $r$ ou du diamètre $D$.

Il vous suffira d'appliquer la formule correspondant aux données de l'énoncé de votre exercice.

Avec le rayon r

Par exemple, si l'on veut calculer le volume d'une boule (ou sphère pleine) de rayon $r = 25cm$, on a :

$V_{boule}= \dfrac{4}{3} \times \pi \times r^3= \dfrac{4}{3} \times \pi \times 25^3= \dfrac{4 \times 3{,}14 \times 15625}{3} = \dfrac{196 250}{3} = \boxed{65416{,}66cm^3}$

Avec le diamètre D

Si l'énoncé de l'exercice ne vous donne que le diamètre $D$ de la boule ou de la sphère, deux solutions s'offrent alors à vous.

1. Diviser $D$ par $2$ et obtenir ainsi le rayon $r$ puisque $r = \frac{D}{2}$. Vous n'aurez plus qu'à appliquer la formule $\boxed{V_{boule}=\dfrac{4\pi}{3} \times r^3}$.

2. Appliquer directement la formule avec $D$

Pour calculer le volume d'une sphère pleine ou d'une boule avec son diamètre $D$ exprimé en $cm$, la formule à appliquer est la suivante :

Ainsi, si l'on reprend le même exemple que précédemment. Calculez le volume $V$ en $cm^3$ de la boule de diamètre $50$cm.
On a :
$V_{boule}= \dfrac{\pi}{6} \times D^3= \dfrac{\pi \times D^3}{6} = \dfrac{\pi \times 50^3}{6} = \dfrac{3{,}14 \times 125 0000}{6} = \dfrac{392 500}{6} = \boxed{65416{,}66cm^3}$

On retrouve bien le même résultat que dans l'exemple précédent.

Démonstration

Pour trouver la formule avec le diamètre, nous pouvons partir de la formule avec le rayon.
On sait que :

$\boxed{V_{boule}=\dfrac{4\pi}{3} \times r^3}$.

avec :

• $V$ = volume de la boule (ou sphère pleine)
• $r$ = le rayon de la sphère en cm

et que $\boxed{r =\dfrac{D}{2}}$

Il nous suffit maintenant de remplacer $r$ par $\dfrac{D}{2}$ dans la formule du volume correspondante.

$V_{boule}=\dfrac{4\pi}{3} \times r^3 = \dfrac{4\pi}{3} \times {\bigg(\dfrac{D}{2}\bigg)}^3 = \dfrac{4\pi}{3} \times \dfrac{D^3}{2^3} = \dfrac{4\pi}{3} \times \dfrac{D^3}{8} = \dfrac{4 \pi D^3}{3 \times 8} = \dfrac{4 \pi D^3}{24}$

Maintenant il suffit de simplifier la fraction ainsi obtenue.
$V_{boule}=\dfrac{4 \pi D^3}{24}= \boxed{\dfrac{\pi D^3}{6}}$

Formule calcul du volume d'une demi-sphère

Rien de plus facile que de calculer une demi-sphère, vous pouvez pour cela :

• Calculer tout d'abord le volume d'une sphère pleine ou d'une boule puis le diviser par 2.
• Calculer directement le volume de la demi-sphère à l'aide des formules suivantes.

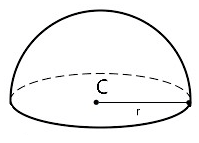
Avec le rayon r

Pour calculer le volume d'une demi-sphère avec le rayon $r$ en cm de cette dernière, la formule est :

Par exemple, si l'on souhaite calculer le volume de la demi-sphère de rayon $25$cm.
On applique la formule :
$V_{demi-sphere}=\dfrac{2 \pi r^3}{3} = \dfrac{2 \pi {25}^3}{3} = \dfrac {2 \pi 15 625}{3} = \dfrac {2 \times 3{,}14 \times 15625}{3} = \dfrac{98 125}{3} = \boxed{32 708 {,}33 cm^3}$

Si l'on multiplie ce résultat par 2, on trouve alors le volume de la boule calculé dans les exemples précédents.

Avec le diamètre D

Si l'énoncé vous fournit la longueur du diamètre $D$ en centimètres, alors vous pourrez appliquer la fomrule suivante :

Reprenons maintenant l'exemple avec le diamètre $D$ de $50cm$. Calculons le volume de la demi-sphère de diamètre $D$.

$V_{demi-sphere}= \dfrac{\pi D^3}{12} = \dfrac{ 3{,}14 \times 50^3}{12} = \dfrac{3{,}14 \times 125 000}{12} = \dfrac{392 500}{12} = \boxed{32 708{,}33 cm^3}$

On trouve bien le même résultat que ci-dessus.

Démonstration

Pour trouver la formule de calcul de la demi-sphère à l'aide du rayon $r$ et du diamètre $D$, il suffit de diviser par 2 les formules de base (puisqu'une demi-sphère est une moitié de sphère ou de boule, son volume correspond à la moitié de celui d'une boule ou sphère pleine normale).

Pour la formule à l'aide du rayon, on a donc :

$V_{demi-sphere}=\dfrac{\frac{4\pi r^3}{3}}{2}$ soit $\dfrac{4\pi r^3}{3} \times \dfrac{1}{2}$

$V_{demi-sphere}= \dfrac{4 \pi r^3}{6}$

Si l'on simplifie par 2, on obtient bien : $V_{demi-sphere}= \dfrac{2\pi r^3}{3}$.

Pour la formule avec le diamètre :
$V_{demi-sphere}=\dfrac{\frac{\pi D^3}{6}}{2}$ soit $\dfrac{\pi D^3}{6} \times \dfrac{1}{2}$

Soit directement notre formule :

$V_{demi-sphere} = \dfrac{\pi D^3}{12}$

Formule de calcul du volume d'une boule creuse

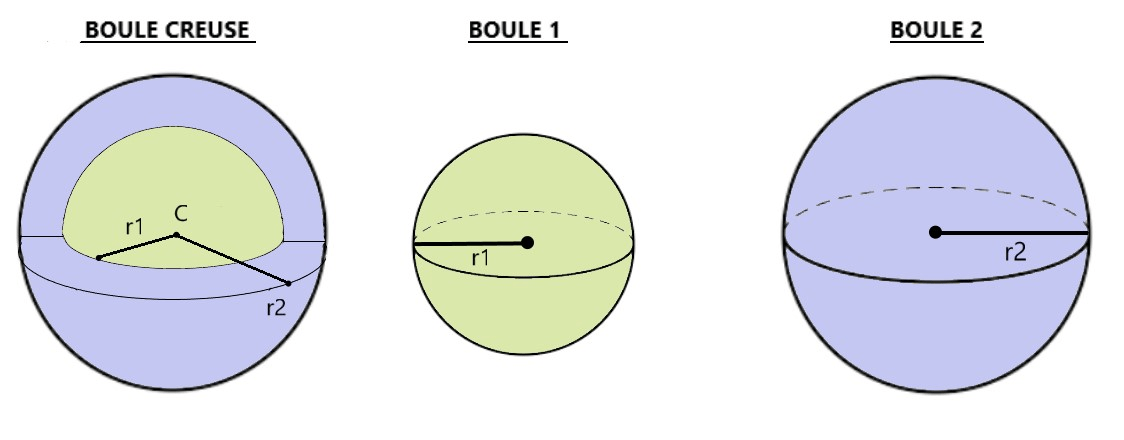
Une boule creuse correspond à deux boules que l'on va emboîter l'une dans l'autre.
Le volume d'une boule creuse correspond au volume représenté en "violet" sur l'illustration de la Boule creuse ci-dessus.

Pour trouver ce volume, il faut donc soustraire le volume de la Boule 2 à celui de la Boule 1.

Démonstration

Pour démontrer la formule ci-dessus, nous allons partir de la déduction précédente. Pour trouver le volume d'une boule creuse, il faut soustraire le volume de la Boule 2 à celui de la Boule 1.

D'où:
$V_{boulecreuse} = V_{Boule2}-V_{Boule1} = \bigg( \dfrac{4\pi}{3} \times {r_2}^3 \bigg) - \bigg( \dfrac{4\pi}{3} \times{r_1}^3 \bigg)$

Si l'on factorise par $\dfrac{4\pi}{3}$ qui est commun aux deux membres, on obtient :

$\boxed{V_{boulecreuse} = \dfrac{4\pi}{3} \times ({r_2}^3-{r_1}^3)}$

Formule calcul du volume d'une sphère tronquée ou calotte sphérique

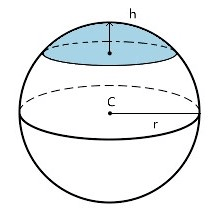
Une sphère tronquée ou calotte sphérique correspond à l'intersection entre la sphère et deux plans parallèles soit une "portion de boule".

Pour calculer le volume de la sphère tronquée (en bleu sur l'illustration), la formule à appliquer est la suivante :

Outils gratuits de calcul du volume d'une sphère

Cette fiche détaille toutes les modalités de calcul du volume d'une sphère.

Cependant, si vous n'avez pas envie de faire les calculs vous-même, ou que vous voulez vérifier les résultats de vos exercices, voici deux outils qui vous serviront à calculer automatiquement (et gratuitement) le volume d'une boule.

Il vous suffira pour cela de rentrer la valeur de son rayon $r$

• Calcul automatique du volume d'une sphère avec Calculer.com
  Sélectionnez "volume d'une sphère" dans Type de volume à calculer, rentrez la valeur du rayon $r$ et sélectionnez l'unité. Cliquez sur Calculer.

• Calcul automatique du volume d'une boule avec Calculette.net
  Même marche à suivre que pour Calculer.com

Outil de conversion en Litres du volume sphère

Si vous souhaitez convertir votre volume de $cm^3$ en $m^3$ ou en $litres$ voici un outil de conversion automatique de volume.

Des exercices pour s'entraîner

Vous avez envie de vous entraîner aux différents calculs de volume de sphère ?

Calculer le volume $V$ en $cm^3$ des solides suivants :

• une boule de rayon $10$cm
• une sphère de diamètre $15{,}4$cm
• une demi-sphère de rayon $13{,}2$cm
• une demi-boule de diamètre $6{,}8$cm
• une boule creuse avec $r_1 = 3$cm et $r_2=5$cm
• une boule creuse avec $D_1 = 6=cm et $D_2=10$cm
• une calotte sphérique de rayon $3$cm et de hauteur $2{,}4$cm
• une sphère tronquée de rayon $4{,}7$cm et de hauteur $8cm$

Exercices complémentaires

Nous vous proposons également plusieurs exercices sur les sujets suivants :

• Un calcul de volume d'une sphère
• Calcul de volume demi-boule et cône en Litres
• Calcul du volume d'un cylindre emboîté dans une sphère
• Fonctions et volume d'une bille sphérique
• Calcul et comparaison du volume d'une boule et d'un cylindre
• Calculer le volume d'une calotte sphérique de hauteur inconnue

Outils supplémentaires

• Pour calculer l'aire ou la surface d'une sphère, il vous suffit de sélectionner sphère sur ce calculateur d'aire gratuit et automatique.