Calculer le volume d'un cylindre

Profitez d'un outil gratuit pour calculer le volume d'un cylindre de révolution et retrouvez la formule ainsi qu'un cours complet pour faire le calcul par vous-même.

En mathématiques, le calcul du volume d'un cylindre est abordé en même temps que les aires et peut parfois poser problèmes aux élèves de 3ème.

Alors, comment faire pour calculer rapidement et facilement le volume d'un cylindre ? Et comment convertir ce volume en litres ?

Toutes les réponses à vos questions sont dans cette fiche-méthode.

Propriétés d'un cylindre

Un cylindre de révolution ou cylindre circulaire droit est un solide.

Le cylindre de révolution est reconnaissable grâce à :

ses bases : deux disques superposables et parallèles
une face latérale perpendiculaire aux bases s'enroulant autour de ses dernières.

Un cylindre est caractérisé par :

son rayon $r$
sa hauteur $h$ (soit la distance entre les centres respectifs des deux bases du cylindre)

Formule calcul du volume d'un cylindre plein

Il existe plusieurs formules pour calculer le volume d'un cylindre. Elles varient en fonction des informations qui sont données dans l'énoncé de l'exercice.

On distingue notamment trois cas de figures différents pour le calcul du volume d'un cylindre : la valeur du rayon $r$ est donnée, la valeur du diamètre $D$ est donnée ou la valeur de l'aire $A$ est donnée.

Pour le calcul du volume du cylindre, il convient de faire attention à ce que $r$ (rayon), $D$ (diamètre) et $h$ (hauteur) soient exprimés dans la même unité.

Par exemple, si $r$ est en $cm$ et $h$ en m, il faudra réaliser une conversion de l'un ou de l'autre pour que tous deux soient exprimés uniquement en $m$ ou en $cm$ .

Le volume est d'abord exprimé en $cm^3$ ou $m^3$ en fonction de l'unité choisie lors du calcul.

Il peut ensuite être converti en litres si besoin est.

Formule avec le rayon $r$

Dans ce cas, l'énoncé-type ressemble au suivant :

Le cylindre est de rayon $r$ 5cm et de hauteur $h$ 8cm.
Calculer son volume $V$ .

Pour répondre à cette question, la formule à appliquer est la suivante.

$\boxed{V_{cylindre} = h \times \pi \times rayon^2 = h \times \pi \times r^2 = h\pi r^2 }$ $(1)$

(Petite astuce mnémotechnique : hache pi-erres carrées)

avec :

$V$ = volume du cylindre
$r$ = rayon du cylindre
$h$ = hauteur du cylindre
$\pi= 3{,}14$

Ici, le volume $V$ du cylindre de rayon $r$ 5 cm et de hauteur $h$ 8 cm est :
$V = 8 \times \pi \times 5^2 = 8 \times 3{,}14 \times 25 = 628 cm^3$ .

Formule avec le diamètre $D$

Dans ce cas, l'énoncé-type ressemble au suivant :

Calculez le volume $V$ du cylindre de diamètre $D$ 30cm et de hauteur $h$ 1m.

Pour répondre à cette question, la formule à appliquer est la suivante.

$\boxed{V_{cylindre} = \dfrac{π}{4} \times D^2 \times h}$ $(2)$

avec :

$V$ = volume du cylindre
$D$ = diamètre du cylindre
$h$ = hauteur du cylindre
$\pi = 3{,}14$

Ici, le volume $V$ est égal à :
$V_{cylindre}= \dfrac{π}{4} \times 30^2 \times 100= \dfrac{3{,}14}{4} \times 900 \times 100 = 70 650 cm^3$

Démonstration des formules

Pour rappel, le rayon $r$ du cercle correspond à la moitié du diamètre $D$ , soit
$\boxed{r = \dfrac {D}{2}}$ .

Inversement, le diamètre $D$ du cercle correspond au double du rayon $r$ , soit $\boxed{D = r \times 2 = 2r}$ .

Ainsi on voit bien que les deux formules de calcul du volume d'un cylindre (que ce soit à l'aide du rayon ou du diamètre) sont équivalentes.

Si $r=\dfrac{D}{2}$ , alors, en remplaçant $r$ , la formule $(1)$ équivaut à :

$V_{cylindre} = h\pi r^2 = h \pi \bigg(\dfrac{D}{2}\bigg)^2 = h \pi \dfrac{D^2}{4}= \dfrac{D^2 h \pi}{4} =$ $\boxed{\dfrac{π}{4} \times D^2 \times h}$ soit la formule $(2)$ .

Si l'on refait le calcul pour le cylindre de diamètre $30$ cm et de hauteur $1$ m en prenant $r$ , on obtient le même résultat.

Soit $r= D/2$ , ici $r = 30/2$ donc $r=15 cm$ , on a :
$V_{cylindre}= h \times \pi \times r^2= 100 \times 3{,}14 \times 15^2 = 100 \times 3{,}14 \times 225 = 70 650 cm^3$

Formule avec l'aire du cercle

Pour calculer le volume d'un cylindre, il existe également une technique avec l'aire $A$ de la base du cylindre.

Si l'on veut calculer le volume $V_{cylindre}$ , on a :

$\boxed{V_{cylindre}= A_{base} \times h = Ah}$ $(3)$

Par exemple, on pourrait vous demander dans le cadre d'un exercice de calculer dans un premier temps l'aire $A$ du cercle de rayon $5cm$ , puis de calculer le volume $V$ du cylindre de rayon $5cm$ et de hauteur $8cm$ .

On aurait donc :
$A = \pi r^2 = 3{,14} \times 5^2 = 3{,14} \times 25 =$ $\boxed{78{,}5cm^2}$

Puis à l'aide de $A$ , on calcule $V_{cylindre}$ .

$V_{cylindre} = Ah = 78{,}5 \times 8 =$ $\boxed{628 cm^3}$

Démonstration de la formule

Si l'on reprend la formule $(1)$ de calcul du volume $V_{cylindre}$ , on a :

$\boxed{V_{cylindre} = h\pi r^2 }$ $(1)$

Or la base du cylindre est un cercle de rayon $r$ . On sait que pour calculer l'aire d'un cercle la formule est la suivante $A_{cercle}= A_{base} = \pi r^2$ .

Par conséquent, $\boxed{V_{cylindre} = h\pi r^2 = h \times A = Ah = Formule (3)}$

Formule calcul du volume d'un cylindre creux

Un cylindre creux consiste en une imbrication de deux cylindres, un grand cylindre et un plus petit cylindre à l'intérieur de ce dernier.

Pour calculer le volume du cylindre creux, il convient de soustraire le volume du grand cylindre à celui du petit cylindre.

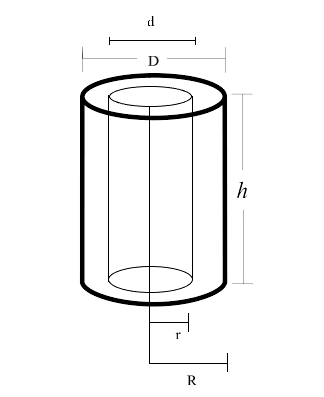
cylindre creux

Avec le diamètre

$V_{cylindre creux} = \dfrac{\pi}{4} \times h (D^2 - d^2)$

avec :

V = volume du cylindre
D = diamètre du grand cylindre
d = diamètre du petit cylindre
$\pi = 3{,}14$

Avec le rayon

$V_{cylindrecreux}= \pi h (R^2 - r^2)$

avec :

V = volume du cylindre
R = rayon du grand cylindre
r = rayon du petit cylindre
$\pi = 3{,}14$

Formule calcul du volume d'un cylindre tronqué

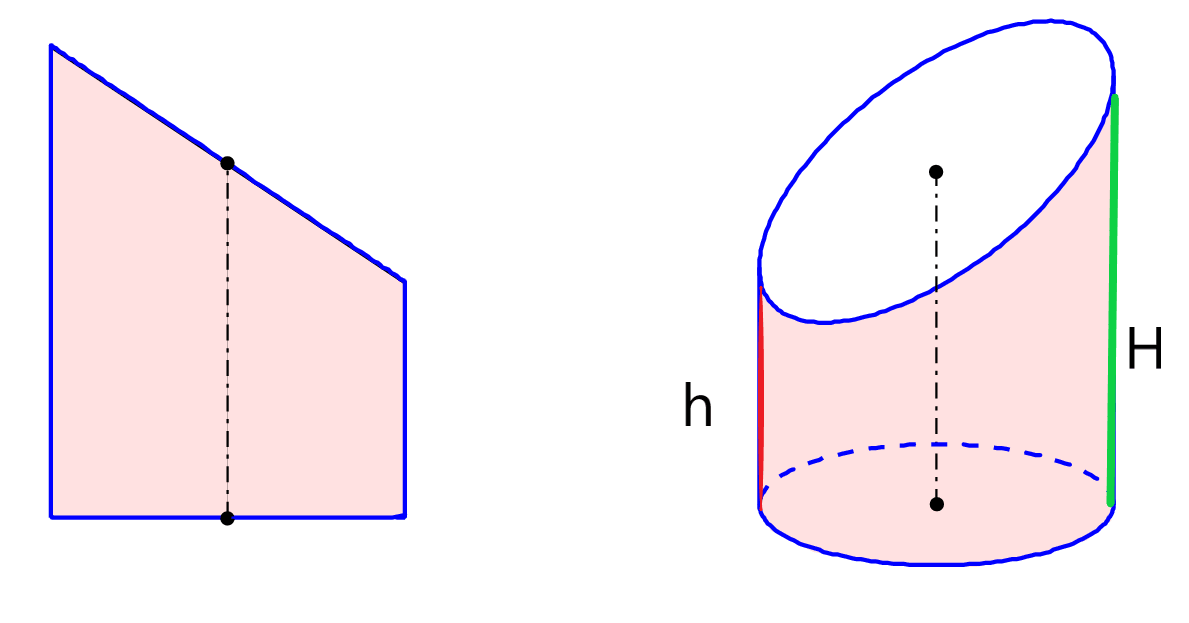
cylindre tronqué

$V_{cylindretronqué}=\dfrac{\pi \times R^2 \times (H + h)}{2}$ .

avec :

V = volume du cylindre
H = plus grande hauteur (en vert sur le dessin)
h = plus petite hauteur (en rouge sur le dessin)
$\pi = 3{,}14$

Formule calcul volume cône tronqué

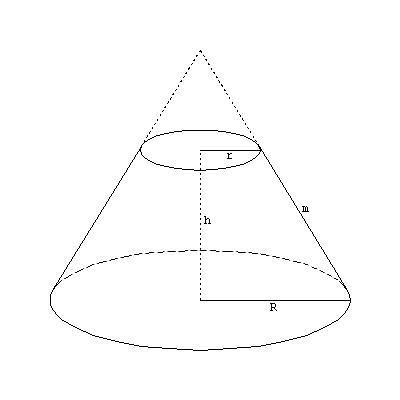
cône tronqué

$V_{cône tronqué} = (h \times \dfrac{\pi}{3}) \times ( R^2 + r^2 + R \times r )= \dfrac{ h \pi}{3} ( R^2 + r^2 + R \times r )$

avec :

V = volume du cylindre
R = plus grand rayon
r = plus petit rayon
$\pi = 3{,}14$

Convertir le volume $V$ du cylindre en Litres

Une fois que vous avez calculé votre volume $V$ en $cm^3$ ou en $m^3$ , voici comment convertir $V$ en litres si ceci vous est demandé.

$1m^3 = 1000 L$ .
$1cm^3 = 0{,}001L$ .

Ainsi, si l'on reprend le résultat $V_{cylindre} = 628 cm^3$ et que on l'exprime en $L$ , on a :
$V_{cylindre} = 628 cm^3$
$1cm^3 = 0{,}001L$

d'où :

$V_{cylindre} = 628 cm^3 = 628 \times 0{,}001 =$ $\boxed{ 0{,}628 L}$ .

Des exercices pour s’entraîner

Vous avez envie de vous entraîner à calculer le volume d'un cylindre ?
Voici quelques exemples pratiques avec différentes valeurs pour le rayon, le diamètre, la hauteur et l'aire.

Calculer le volume $V$ du cylindre exprimé en $cm^3$ :

du cylindre de révolution de rayon $5cm$ et de hauteur $20cm$
du cylindre de révolution de rayon $6{,}4 cm$ et de hauteur $1m$
du cylindre de révolution de diamètre $20cm$ et de hauteur $34cm$
du cylindre de révolution de diamètre $4cm$ et de hauteur $1,23m$
du cylindre de révolution dont l'aire $A$ de la base est de $57cm^2$ et la hauteur $h$ est de $12cm$ .
du cylindre de révolution dont l'aire $A$ de sa base est de $33cm^2$ et la hauteur $h$ est de $0{,}76m$

Exprimer ces volumes en $L$ .

Outils de calcul du volume d'un cylindre

Cette fiche détaille toutes les modalités de calcul du volume d'un cylindre.

Cependant, si vous n'avez pas envie de faire les calculs vous-même, voici deux outils qui vous serviront à calculer automatiquement (et gratuitement) le volume d'un cylindre de révolution. Il vous suffira pour cela de rentrer la valeur de son rayon $r$ et de sa hauteur $h$ avec les mêmes unités.

Outil de conversion volume cylindre

Si vous souhaitez convertir votre volume de $cm^3$ en $m^3$ ou en $litres$ voici un outil de conversion automatique de volume.

Exercices complémentaires

Nous vous proposons également un exercice où vous aurez, entre autres, à calculer le volume d'un cylindre.

Calculer le volume d'un cylindre

Propriétés d'un cylindre