Calcul du volume d'une pyramide

Retrouvez la formule ainsi qu'un cours complet pour faire le calcul du volume d'une pyramide par vous-même.
Et profitez d'un outil gratuit pour calculer automatiquement l'aire de la base de la pyramide ainsi que pour convertir le volume en litres.

En mathématiques, le calcul du volume et des aires des solides est abordé au même moment et peut parfois poser des difficultés aux élèves.

Propriétés d'une pyramide

Comment reconnaître une pyramide ?

Une pyramide est un polyèdre. La particularité de la pyramide est que l'une de ses faces, également appelée la base, est un polygone.
Les autres faces de la pyramide sont des triangles.

Selon la nature de la base, on parle de pyramide à base triangulaire ou carrée ou rectangulaire, pentagonale, ...

Une pyramide possède autant de faces latérales que sa base a de côtés
Par conséquent, si la base de la pyramide est un carré (4 côtés), alors la pyramide aura $4$ faces. Si la base de la pyramide est triangulaire, alors la pyramide aura $3$ faces.
La distance entre le sommet et le plan de base est appelée la hauteur de la pyramide.

Une pyramide est donc caractérisée par :

sa base polygonale et la forme de cette dernière (triangle, carré, rectangle...)
sa hauteur $h$

Formule générale de calcul du volume d'une pyramide avec l'aire de sa base

Pour calculer correctement le volume de l'aire d'une pyramide, il convient d'identifier la forme de sa base : est-elle carrée ? rectangulaire ? triangle ?

A partir de là vous trouverez ci-dessous les formules de calcul du volume d'une pyramide en fonction de la forme de sa base.

La formule générale de calcul du volume d'une pyramide met en lien l'aire de la base de la pyramide et la hauteur de cette dernière.

$\boxed{V_{pyramide} = \dfrac{Aire_{base} \times h}{3}}$

avec :

$V$ = volume de la pyramide
$h$ = hauteur de la pyramide
$Aire_{base}$ = l'aire de la base de la pyramide

Calcul du volume d'une pyramide à base rectangulaire

Il existe deux méthodes pour calculer le volume d'une pyramide à base rectangulaire.

Pour ce calcul de volume, il est ainsi possible d'utiliser :

L'aire de la base ici l'aire d'un rectangle
La longueur et la largeur du rectangle à la base de la pyramide

Formule avec l'aire du rectangle

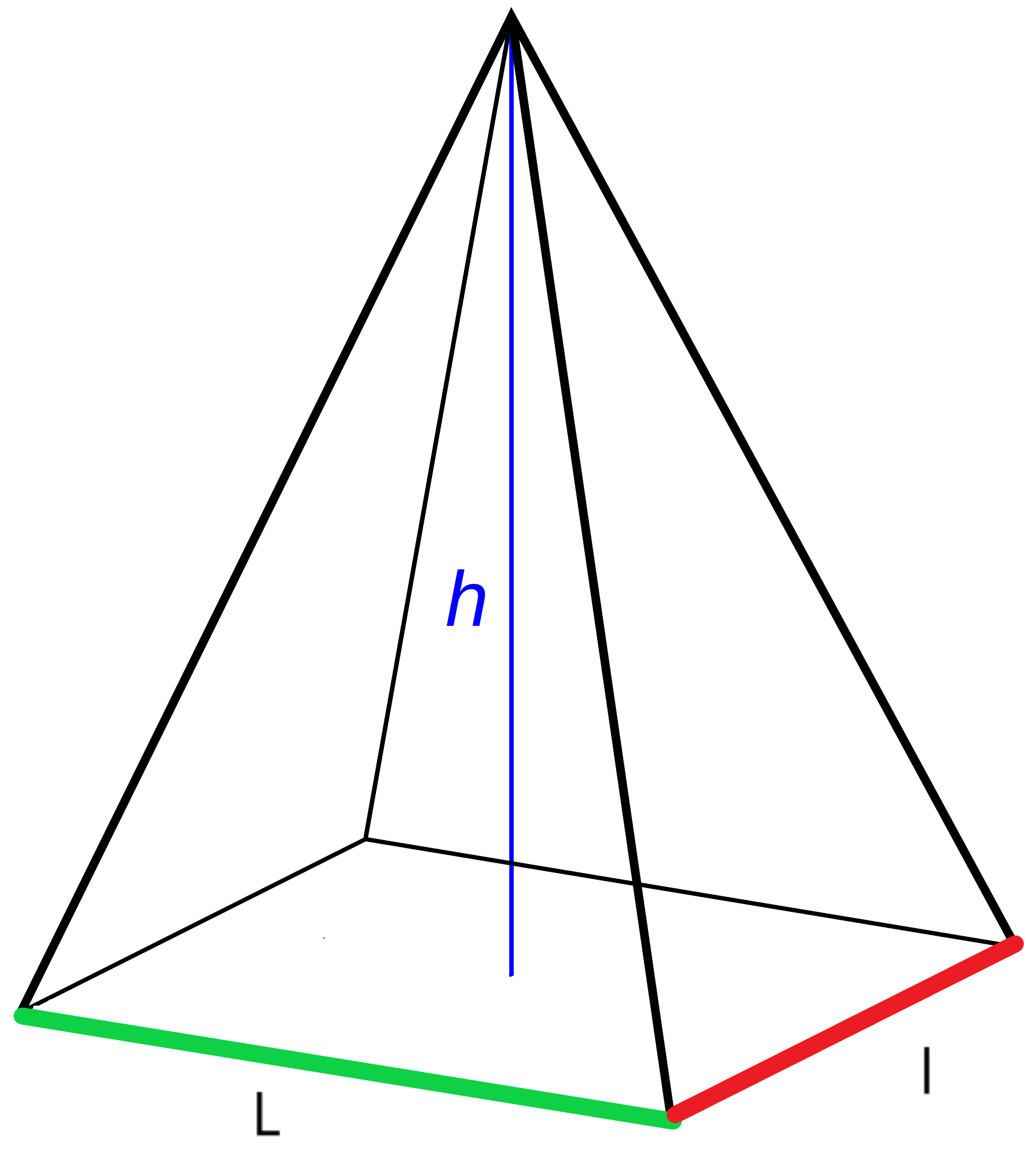
pyramide base rectangulaire

$V_{pyramidebaserectangle} = \dfrac{Aire_{rectangle} \times h}{3}$

avec :

$A$ = aire de la base $= Aire_{rectangle}= L \times l$
$L$ = longueur du rectangle
$l$ = largeur du rectangle
$h$ = hauteur de la pyramide

Un exercice portant sur le calcul du volume d'une pyramide à base rectangulaire pourrait comporter un énoncé-type comme suit.

La pyramide suivante est une pyramide à base rectangulaire. L'aire $A$ de sa base fait $20cm^2$ et dont la hauteur $h$ mesure $5cm$ .
Calculez le volume de la pyramide.

$V_{pyramide} = \dfrac{Aire_{rectangle} \times h}{3}= \dfrac{20 \times 5}{3} = \dfrac{100}{3} \boxed{\approx 33{,}3 cm^3}$

Formule avec la longueur et la largeur du rectangle

Pour avoir la formule directement applicable avec les mesures de la longueur et de la largeur du rectangle qui sert de base à la pyramide, on remplace $A_{rectangle}$ par $l \times L$

$V_{pyramide base rectangulaire} = \dfrac{l \times L \times h}{3}= \boxed{\dfrac{Llh}{3}}$

avec :

$L$ = longueur du rectangle
$l$ = largeur du rectangle
$h$ = hauteur de la pyramide

Par exemple, calculez le volume de la pyramide à base rectangulaire de longueur $L$ $5cm$ , de largeur $l$ $4cm$ et de hauteur $h$ , $5cm$ .

$V_{pyramidebaserectangle} = \dfrac{L \times l \times h}{3} = \dfrac{5 \times 4 \times 5}{3} = \dfrac{100}{3} \approx \boxed{33{,}3cm^3}$

Calcul du volume d'une pyramide à base carrée

Pour calculer le volume d'une pyramide à base carrée, il est également possible de se servir de l'aire de la base donc de l'aire du carré ou bien de la longueur d'un des côtés du carré.

Formule avec l'aire du carré

$V_{pyramide base carrée} = \boxed{\dfrac{A_{carré} \times h}{3}}$

avec :

$A$ = aire de la base $= Aire_{carré}= c \times c = c^2$
$c$ = longueur d'un côté du carré
$h$ = hauteur de la pyramide

Par exemple, si l'énoncé est le suivant : calculez le volume de la pyramide à base carrée dont l'aire de la base est $25cm^2$ et la hauteur est $6cm$ .

Il suffit d'appliquer directement la formule comme suit :

$V_{pyramidebasecarrée}= \dfrac{A_{carré} \times h}{3} = \dfrac{25 \times 6}{3} = \dfrac{150}{3} = \boxed{50cm^3}$

Formule avec la longueur d'un côté du carré

Pour avoir la formule directement applicable avec $c$ s'il est donné dans l'énoncé, on remplace $A_{carré}$ par $c^2$ soit :

$V_{pyramide base carrée} = \boxed{\dfrac{c^2 \times h}{3}}$

avec :

$c$ = longueur d'un côté du carré
$h$ = hauteur de la pyramide

Dans le cadre des énoncés d'exercices, il sera généralement demandé de calculer d'abord l'aire de la base de la pyramide et ensuite son volume total.

Cependant, si l'on vous demande directement le volume de la pyramide et que l'énoncé ne comprend que la longueur d'un côté de la base (ici carrée), alors vous pouvez vous servir de la formule ci-dessus.

Par exemple, calculez le volume de la pyramide de base carrée dont la longueur $c$ du côté mesure $5cm$ et la hauteur $6cm$ .

$V_{pyramidebasecarrée} = \dfrac{5^2 \times 6}{3} = \dfrac{25 \times 6}{3} = \dfrac{150}{3} = \boxed{50cm^3}$

Calcul volume pyramide base triangulaire

Pour un triangle quelconque ou rectangle, il suffit d'appliquer la formule générale soit :

$\boxed{V_{pyramidebasetriangulaire} = \dfrac{Aire_{base} \times h}{3}= \dfrac{Aire_{triangle} \times h}{3}}$

avec :

$V$ le volume de la pyramide
$Aire_{triangle}$ l'aire du triangle ainsi calculée
$h$ la hauteur de la pyramide

Par exemple, si l'énoncé d'un exercice précise :

La pyramide $ABCD$ est de base triangulaire $ABC$ dont l'aire est de $4cm^2$ et la hauteur de $6cm$ . Calculez le volume de la pyramide $ABCD$ .

Il suffira alors d'appliquer directement la formule :
$V_{ABCD} = \dfrac{Aire_{ABC} \times h}{3} = \dfrac {4 \times 6}{3} = \dfrac{24}{3} = \boxed{8cm^3}$

La plupart du temps, il vous sera en premier lieu demandé de calculer l'aire du triangle de base puis ensuite le volume.

Pour ce faire, il suffit de se rappeler de la formule pour calculer l'aire d'un triangle.

$Aire_{triangle}= \dfrac{Base_{triangle} \times hauteur_{triangle}}{2} = \dfrac{ B \times h_{triangle}}{2} = \dfrac {Bh_{triangle}}{2}$

avec :

$B$ la base, (en bleu sur le dessin)
$h$ la hauteur (en rouge)

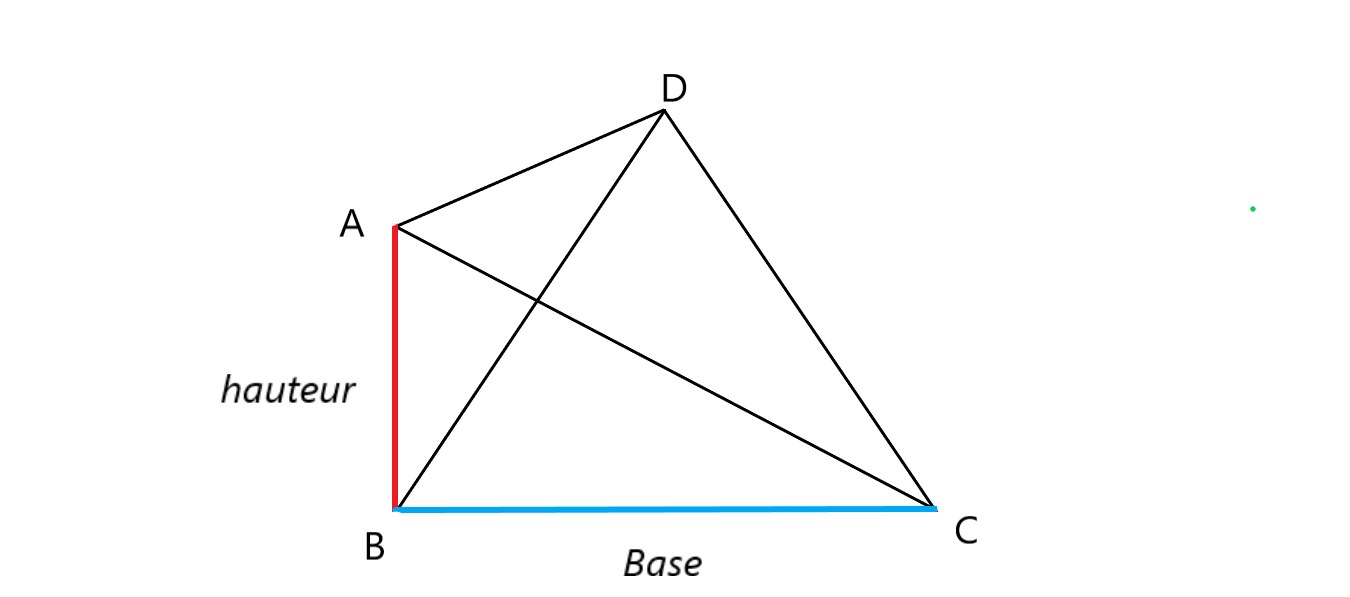
Pyramide base triangulaire

Pour un triangle rectangle, il peut arriver que l'on demande d'appliquer Pythagore pour pouvoir calculer l'aire avant de passer à l'application de la formule du volume.

Calcul volume pyramide tronquée

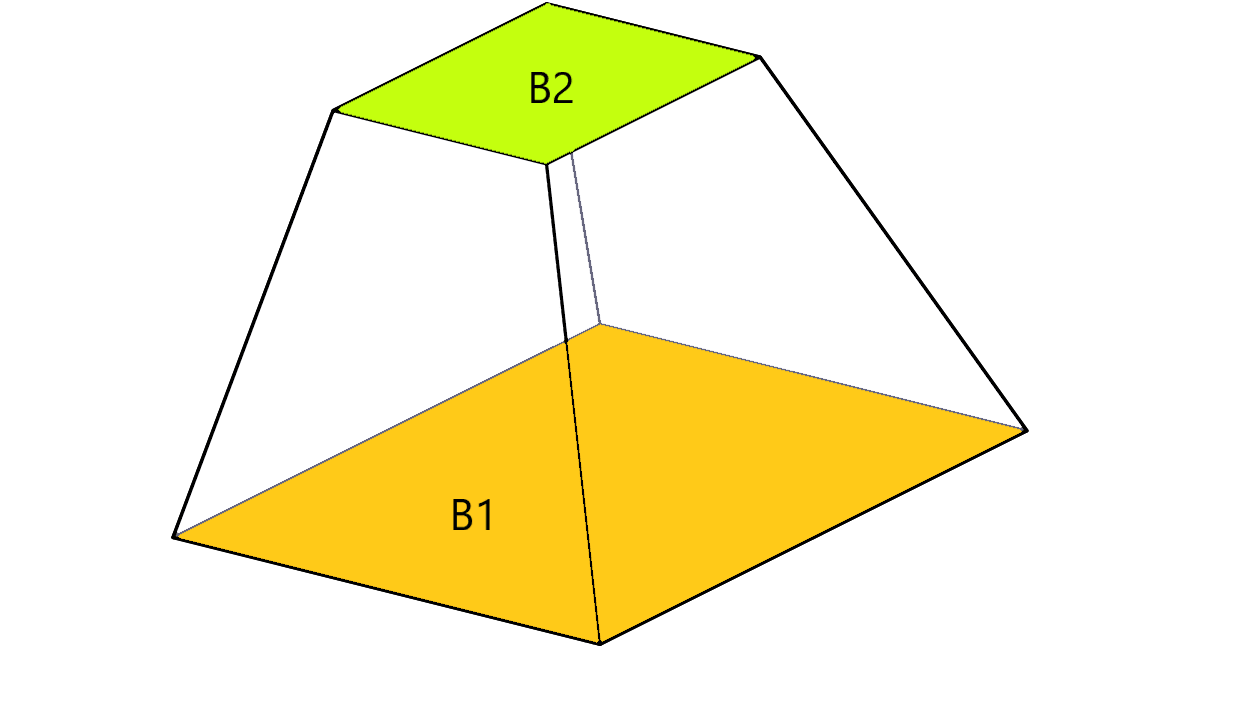
Pour calculer le volume d'une pyramide tronquée, la formule à appliquer est la suivante :

$V_{pyramidetronquée} = \dfrac{(B_1 + B_2 + \sqrt{B_1 \times B_2}) \times h}{3}$

avec :

$B_1$ l'aire de la base 1 de la pyramide tronquée
$B_2$ l'aire de la base 2 de la pyramide tronquée
$h$ la hauteur de la pyramide tronquée

Le cas particulier du cône de révolution : calcul du volume d'une pyramide à base ronde

Une pyramide est un solide avec un polygone pour base et des faces latérales triangulaires.

Par conséquent, une "pyramide à base ronde" n'existe pas.
On appelle ce cas particulier un cône de révolution.

cone_de_révolution

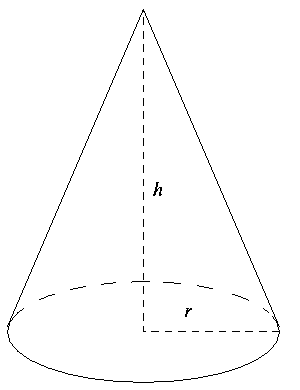
Avec l'aire du disque

Cependant, la formule à appliquer est exactement la même que pour les pyramides soit :

$\boxed{V_{cônede révolution} = \dfrac{Aire_{base} \times h}{3} = \dfrac {Aire_{cercle} \times h}{3}}$

Avec le rayon du disque

Si l'énoncé de l'exercice ne précise que le rayon $r$ du disque de base du cône de révolution ainsi que sa hauteur $h$ , alors il faudra appliquer la formule suivante :

$\boxed{V_{cônede révolution} = \dfrac {Aire_{cercle} \times h}{3} = \dfrac{\pi r^2 \times h }{3}}$

Ainsi, pour calculer le volume d'un cône de révolution dont le disque de base mesure $2cm$ de rayon et la hauteur $6cm$ , il convient de procéder comme suit :

$V_{cônede révolution} = \dfrac{\pi r^2 \times h }{3} = \dfrac{\pi 2^2 \times 6 }{3} = \dfrac{24 \pi}{3} = 8 \pi cm^3 \approx 25{,}12 cm^3$

Convertir le volume $V$ du cube en Litres

Une fois que vous avez calculé votre volume $V$ en $cm^3$ ou en $m^3$ , voici comment convertir $V$ en litres si ceci vous est demandé.

$1m^3 = 1000 L$ .
$1cm^3 = 0{,}001L$ .

Ainsi, si l'on reprend le résultat $V_{cube} = 125cm^3$ et que on l'exprime en $L$ , on a :
$V_{cube} = 125 cm^3$
$1cm^3 = 0{,}001L$

d'où :

$V_{cube} = 125 cm^3 = 125 \times 0{,}001 =$ $\boxed{ 0{,}125 L}$ .

Des exercices pour s’entraîner

Vous avez envie de vous entraîner à calculer le volume d'une pyramide ?

Voici quelques exercices pratiques pour vous.

Calculer le volume $V$ de la pyramide exprimé en $cm^3$ :

une pyramide de base rectangulaire (largeur $l$ = $7cm$ et longueur $L$ = $8{,}5cm$ ) de hauteur $4cm$
une pyramide de base carrée, dont l'un des côtés de la base fait $3cm$ et de hauteur $10cm$ .
une pyramide de base triangulaire dont l'aire fait $13cm^2$ et la hauteur $9cm$ .

Exprimez ces volumes en $L$ .

Outils de calcul de l'aire de la base de la pyramide

Cette fiche détaille toutes les modalités de calcul du volume d'une pyramide.

Cependant, si vous n'avez pas envie de faire tous les calculs vous-même, voici deux outils qui vous serviront à calculer automatiquement (et gratuitement) l'aire de la base de la pyramide. Vous n'aurez plus qu'à multiplier par la hauteur de la pyramide pour obtenir le volume de cette dernière

Pour ce faire, il suffit de suivre les instructions indiquées en fonction de la forme de la base de la pyramide en question.

Outil de conversion du volume en Litres

Si vous souhaitez convertir votre volume de $cm^3$ en $m^3$ ou en $litres$ voici un outil de conversion automatique de volume.

Exercices complémentaires

Voici notre sélection complémentaire d'exercices sur le volume d'un cube.

un exercice portant sur le calcul du volume d'une pyramide
un exercice sur la fonction de volume maximal
un autre exercice portant sur les fonctions et le volume d'une pyramide
un dernier exercice sur le calcul du volume d'une pyramide tronquée

Calcul du volume d'une pyramide

Propriétés d'une pyramide

Formule générale de calcul du volume d'une pyramide avec l'aire de sa base