Fonctions exponentielles et logarithme pour Terminale S

Voici un condensé de cours et un extrait du support d'exercices et d'annales de mathématiques corrigés, traitant de de la fonction exponentielle, logarithme népérien et logarithme décimal.

Ces documents ont été mis à disposition par Groupe Réussite durant notre stage intensif de préparation au bac S pour les élèves de Terminale S qui se destinent aux classes préparatoires (prépas HEC, prépas scientifiques maths sup et maths spé) ou à des filières sélectives (médecine, Sciences Po, etc).

Ces exercices difficiles ne constituent pas du hors-programme mais simplement des entraînements plus formateurs en vue de l'année de prépa.

Pour accéder au résumé de cours et méthodes, veuillez cliquer ici

1.1 Fonction exponentielle

Définition et propriété : fonction exponentielle

La fonction exponentielle est l'unique fonction $f$ , dérivable sur $\mathbb{R}$ , telle que :

$f'=f$ et $f(0) =1$

Propriété

La fonction exponentielle, notée $exp$ , vérifie :

$\forall$ $x$ , $y$ $\in$ $\mathbb{R}$ , $exp (x+y)$ = $exp(x) \times exp(y)$

et il existe un unique réel noté $e$ ( $\approx$ $2{,}718$ ), tel que $exp(e) = 1$

On démontre alors que la fonction exponentielle vérifie la notation suivante :

$\forall$ $x$ $\in$ $\mathbb{R}$ , $exp (x)$ = $e^x$

Propriété : signe et variations

La fonction exponentielle est strictement positive sur $\mathbb{R}$ :

$\forall$ $x$ $\in$ $\mathbb{R}$ , $e^x >0$

La fonction exponentielle est strictement croissante sur $\mathbb{R}$ . Donc pour tout réels $x$ et $y$ :

$x$ < $y$ $\Longleftrightarrow$ $e^x$
$x = y$ $\Longleftrightarrow$ $e^x = e^y$

Propriétés algébriques

Pour tous réels $x$ , $y$ et pour tout entier $n$ :

$e^{x+y} = e^x \times e^y$
$e^{-x} = \dfrac{1}{e^x}$
$e^{x-y} = \dfrac{e^x}{e^y}$
$e^{\frac{x}{2}} =\sqrt{e^x}$
$(e^x)^n = e^{nx}$

Limites

$\lim\limits_{x \rightarrow +\infty} e^x$ = $+\infty$
$\lim\limits_{x \rightarrow -\infty} e^x$ = $0$
$\lim\limits_{x \rightarrow +\infty} \dfrac{e^x}{x}$ = $+\infty$
$\lim\limits_{x \rightarrow -\infty} xe^x$ = $0$

(On dit que la fonction exponentielle domine les fonctions polynomiales)

$\lim\limits_{h \rightarrow 0} \dfrac{e^h-1}{h}$ = $1$

Dérivée

La fonction exponentielle est dérivable (donc continue) sur $\mathbb{R}$ , et pour tout réel $x$ :

$exp'(x) = exp(x) =e^x$

L'approximation affine au voisinage de $0$ de la fonction exponentielle est $h \longrightarrow 1 +h$ .

On écrira :

$e^h \sim 1+h$ , pour $h$ proche de $0$ .

Si $u$ est une fonction dérivable sur un intervalle $I$ , alors la fonction $e^n$ est dérivable sur $I$ et, pour tout $x$ de $I$ :

$(e^u)'(x) = u'(x)e^{u(x)}$

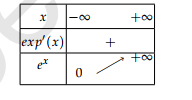
Tableau de variations et courbe

Tableau de variations

Courbe

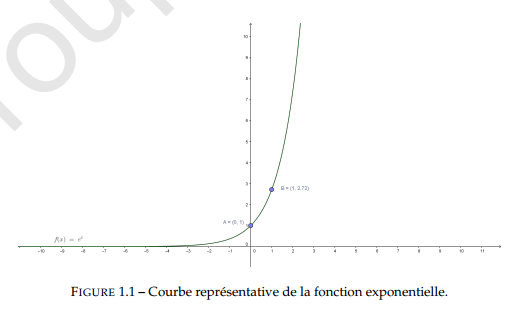
La tangente au point d'abscisse $0$ a pour équation : $y=x+1$ .

La tangente au point d'abscisse $1$ a pour équation : $y=ex$ (elle passe par l'origine).

Résolution d'équations

Equation : $e^x=y$

Pour tout réel $y$ strictement positif, l'équation $e^x=y$ , d'inconnue $x$ , admet une unique solution dans $\mathbb{R}$ .

Equation différentielle d'ordre 1 : $f'=kf$ , avec $k \in \mathbb{R}$ (hors programme)

Soit $k \in \mathbb{R}$ . Les fonctions $f$ dérivables sur \mathbb{R} qui vérifient : $f'=kf$ sont les fonctions $x \rightarrow Ae^{kx}$ , avec $A \in \mathbb{R}$ .

1.2 Fonctions logarithmes népérien et décimal

Définition

La fonction logarithme népérien, notée $ln$ , est la bijection réciproque de la fonction exponentielle. Elle est définie sur $]0;+\infty[$ , et vérifie :

$\forall$ $x$ $\in ]0;+\infty[$ , $\forall$ $y$ $\in \mathbb{R}$ , $y=ln(x) \Longleftrightarrow e^y =x$

Premières Propriétés

La fonction $ln$ a pour ensemble de définition $]0;+\infty[$ et vérifie :

$\forall$ $x$ , $y$ $> 0$ , $ln (x \times y)$ = $ln(x) + ln(y)$
$\forall$ $x$ $\in \mathbb{R}$ , $ln(e^x)=x$
$\forall$ $x> 0$ , $e^{ln(x)}=x$

Signe

La fonction $ln$ est strictement négative sur $]0;1[$ puis strictement positive sur $]1;+\infty[$ .

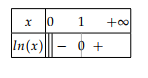
Propriétés algébriques

Pour tous réels $x$ , $y$ dans $]0;+\infty[$ , et tout entier $n$ :

$ln(xy) = ln(x) +ln(y)$

$ln(\dfrac{1}{x}) = -ln(x)$

$ln(\dfrac{x}{y})= ln(x) -ln(y)$

$ln (\sqrt{x})= \dfrac{1}{2} ln(x)$

$ln (x^n) = nln(x)$

Limites

$\lim\limits_{x \rightarrow +\infty} ln(x)$ = $+\infty$

$\lim\limits_{x \rightarrow 0} ln(x)$ = $-\infty$
$\lim\limits_{x \rightarrow +\infty} \dfrac{ln(x)}{x}$ = $0$

$\lim\limits_{x \rightarrow 0} \dfrac{ln(1+h)}{h}$ = $1$

Dérivée et sens de variation

La fonction $ln$ est dérivable (donc continue) sur $]0;+\infty[$ et, pour tout réel $x$ strictement positif :

$ln'(x) = \dfrac{1}{x}$

L'approximation affine au voisinage de $0$ de la fonction $h \longrightarrow ln(1+h)$ est $h \longrightarrow h$ . On écrira :

$ln(1+h) \sim h$ , pour $h$ proche de $0$

La fonction $ln$ est strictement croissante sur $]0;+\infty[$ , donc, pour tous réels $x$ et $y$ de $]0;+\infty[$ :

$x$

$x=y \longleftrightarrow ln(x) = ln(y)$

Si une fonction $u$ est positive et ne s'annule pas sur un intervalle $I$ , alors $ln(u)$ est dérivable sur $I$ et, pour tout $x$ de $I$ :

$(ln(u))'(x) = \dfrac{u'(x)}{u(x)}$

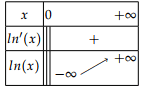
Tableau de variations et courbe

Tableau de variations

La fonction $ln$ est strictement croissante sur $]0;+\infty[$ .

Courbe

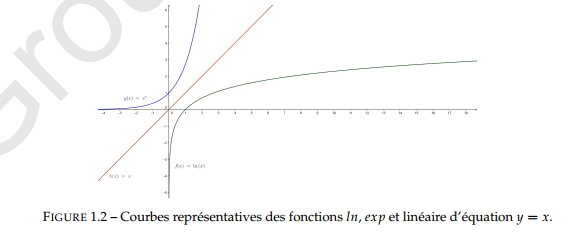
Dans un repère orthonormal, les courbes représentatives des fonctions $exp$ et $ln$ sont symétriques par rapport à la droite d'équation $y=x$ .

Définition (logarithme décimal)

On appelle la fonction logarithme décimal la fonction notée $log$ , et définie sur $]0;+\infty[$ par :

$log(x) = \dfrac{ln(x)}{ln(10}$

Croissance comparée des fonctions exponentielle, puissances entières et logarithme :

Pour tout entier naturel $n$ :

$\lim\limits_{x \rightarrow +\infty} \dfrac{e^x}{x^n}$ = $+\infty$
$\lim\limits_{x \rightarrow -\infty} x^ne^x$ = $0$

(à l'infini, l'exponentielle de $x$ l'emporte sur toute puissance de $x$ )

$\lim\limits_{x \rightarrow +\infty} \dfrac{ln(x)}{x^n}$ = $0$

(en $+\infty$ , les puissances de $x$ l'emportent sur le logarithme de $x$ ).

2. Exercices et Annales

Pour accéder aux exercices et annales traitant de la fonction exponentielle, logarithme népérien et logarithme décimal, veuillez cliquer ici

3. Corrigés d'Exercices

Pour accéder aux corrigés des exercices portant sur de la fonction exponentielle, logarithme népérien et logarithme décimal, veuillez cliquer ici

Fonctions exponentielles et logarithme pour Terminale S

1.1 Fonction exponentielle