Résolutions graphiques dans un repère du plan carthésien
Objectifs
Les nouveaux bacs sont de plus en plus axés sur des résolutions graphiques : lecture du coefficient directeur d'une tangente, résolution d'équation etc.
Ce fichier a été écrit dans le but d'aider les élèves de terminale dans ce genre de questions.
Plan de cours
1 - Lecture d'images
2 - Lecture d'antécédents
3 - Résolution d'équations
4 - Résolution d'inéquations
5 - Tableau de variations
6 - Tableau de signes
7 - Lecture du coefficient directeur d'une droite
8 - Autour de la dérivée
Cours
Avant-propos :
On trouvera dans ce fichier la plupart des techniques de lecture graphiques devant être maîtrisées en analyse. Aucune théorie n'est faite, seuls des exemples sont présentés ainsi que leur correction. Ils feront donc référence pour vous aider dans les exercices.
Ce fichier a été conçu avec l'idée suivante : vous vous trouvez en classe ou chez vous devant une difficulté relevant de la lecture graphique d'une fonction.
Vous ouvrez ce fichier au plan de cours (table des matières) et consultez la section qui vous concerne. Là vous analysez les exemples données pour que vous soyez enfin inspirés pour votre exercice.
L'ordre des exemples a été choisi par difficulté croissante. Ainsi pour comprendre une partie, il est souvent utile de lire la précédente (voir toutes les précédentes!!!).
Important :
On rappelle par ailleurs, que dans l'écriture de , le nombre s'appelle antécédent, et le nombre est l'image du nombre . Graphiquement représente l'abscisse d'un point et son ordonnée. Tous les exemples qui suivent se basent sur cette idée.
1- Lecture d'images
Enoncé
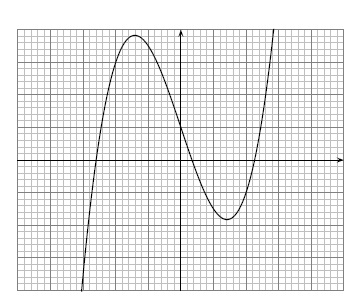
Le graphique ci-dessous représente la courbe d'une fonction sur l'intervalle .
-
Trouver l'image de par .
-
Combien vaut ?
-
Trouver l'image de .
-
Trouver l'image de .
Correction
- 1) Trouver l'image de par .
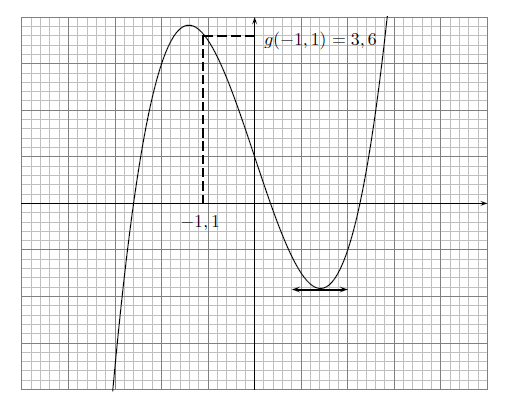
Pour trouver l'image de , on se place sur l'axe des abscisses sur le nombre , on remonte (en pointillés) jusqu'à toucher la courbe.
A ce moment-là, on part à l'horizontale (toujours en pointillés) jusqu'à l'axe des ordonnées. L'image de à savoir , se lit alors sur l'axe des ordonnées.
On a donc :
- 2) Combien vaut ?.
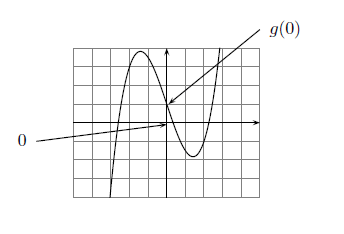
Pour trouver , on se place sur l'axe des abscisses sur le nombre , (à l'origine du repère en fait), on remonte jusqu'à toucher la courbe. On est déjà sur l'axe des ordonnées, il ne reste qu'à regarder où on s'y trouve.
On a donc : , ou formulé autrement : "L'image de par est égale à ".
- 3) Trouver l'image de .
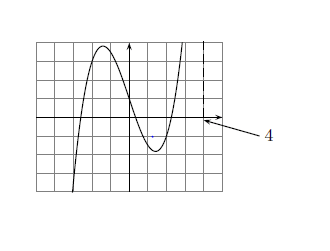
Pour trouver l'image de , on se place sur l'axe des abscisses sur le nombre , on remonte (en pointillés) jusqu'à toucher la courbe...
Mais on ne voit plus la courbe. On ne peut donc pas répondre, car la courbe peut se trouver à peu près n'importe où hors du repère visible.
Il n'y a pas de réponse.
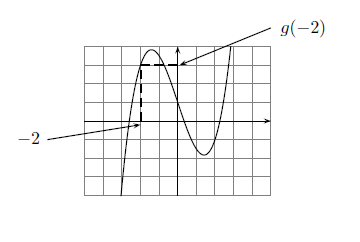
- 4) Trouver l'image de .
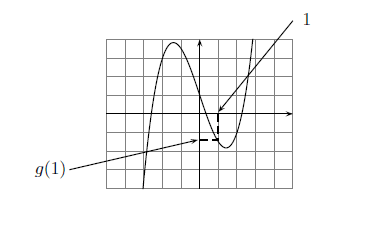
Pour trouver l'image de , on se place sur l'axe des abscisses sur le nombre , on descend (en pointillés) jusqu'à toucher la courbe.
A ce moment-là, on part à l'horizontale (toujours en pointillés) jusqu'à l'axe des ordonnées. L'image de à savoir , se lit alors sur l'axe des ordonnées.
On a donc :
2- Lecture d'antécédents
Enoncé
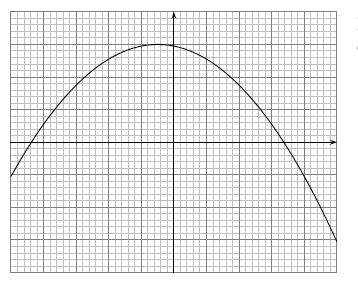
Le graphique ci-dessous représente la courbe d'une fonction sur l'intervalle .
-
Trouver le(s) antécédent(s) de par .
-
Trouver le(s) antécédent(s) de par .
-
Trouver le(s) antécédent(s) de par .
-
Trouver le(s) antécédent(s) de par .
Correction
- 1) Trouver le(s) antécédent(s) de par .
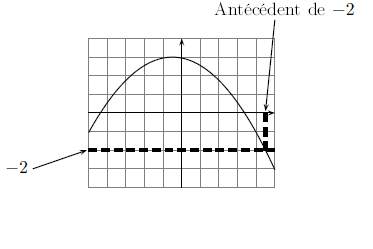
On cherche ici les nombres tels que . C'est-à-dire que l'on cherche l'abscisse (car on cherche un ) d'un point qui se trouve à la hauteur de la courbe.
Pour cela, on trace une droite horizontale à la hauteur (la droite d'équation en fait). Là où cette droite coupe la courbe, on remonte vers l'axe des abscisses. On lit alors la valeur de l'antécédent de .
On a donc uniquement qui est l'antécédent de par . En d'autres termes :
- 2) Trouver le(s) antécédent(s) de par .
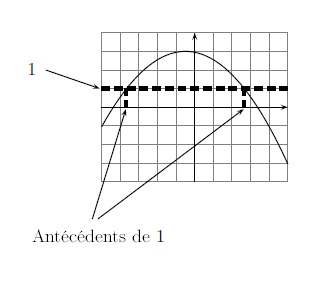
On cherche ici les nombres tels que . C'est-à-dire que l'on cherche l'abscisse (car on cherche un ) d'un point qui se trouve à la hauteur de la courbe.
Pour cela, on trace une droite horizontale à la hauteur (la droite d'équation en fait). Là où cette droite coupe la courbe, on redescend vers l'axe des abscisses. On lit alors la valeur des antécédents de .
On voit donc que possède 2 antécédents : et
- 3) Trouver le(s) antécédent(s) de par .
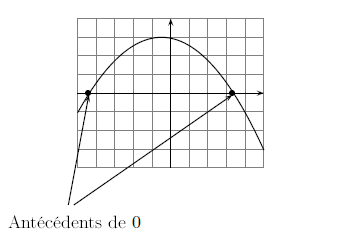
On cherche ici les nombres tels que . C'est-à-dire que l'on cherche l'abscisse (car on cherche un ) d'un point qui se trouve à la hauteur de la courbe.
On cherche donc les points qui sont à la fois sur la courbe et sur l'axe des abscisses. Pas besoin donc de tracer de droite ici.
On voit donc que possède 2 antécédents : et
- 4) Trouver le(s) antécédent(s) de par .
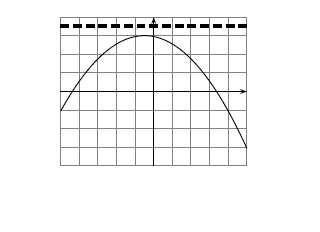
On cherche ici les nombres tels que . C'est-à-dire que l'on cherche l'abscisse (car on cherche un ) d'un point qui se trouve à la hauteur de la courbe.
Pour cela, on trace une droite horizontale à la hauteur (la droite d'équation en fait). Et ici on voit qu'elle ne coupe jamais la courbe de . On ne peut donc pas trouver d'antécédent à dans l'intervalle .
Dans l'intervalle , le nombre ne possède aucun antécédent par .
3 - Résolution d'équations
Enoncé
Le graphique ci-dessous représente la courbe d'une fonction sur l'intervalle .
Résoudre l'équation .
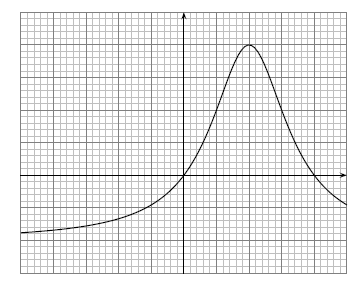
Correction : Résolution de l'équation
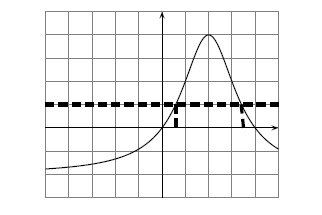
Résoudre veut dire que l'on cherche tel que vaut . Le nombre est une ordonnée, on cherche donc tel que l'on se trouve à la hauteur sur la courbe. Cela revient donc à chercher les antécédents de . Exactement comme dans la partie précédente.
Ainsi l'équation possède 2 solutions et .
On vient donc de remarquer que la résolution d'une équation est exactement une recherche d'antécédent, on se référera ainsi à la partie précédente pour plus d'explications.
4 - Résolution d'inéquations
Enoncé
Le graphique ci-dessous représente la courbe d'une fonction sur l'intervalle .
-
1. Résoudre l'inéquation .
-
2. Résoudre l'inéquation .
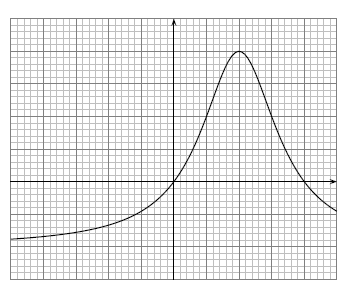
Correction
- 1) Résoudre l'inéquation ..
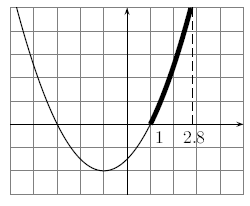
On recherche des nombres qui vérifient . C'est-à-dire que l'on cherche des points dont l'ordonnée est au-dessus de la hauteur (d'équation ). On voit qu'elle coupe la courbe aux points d'abscisse et .
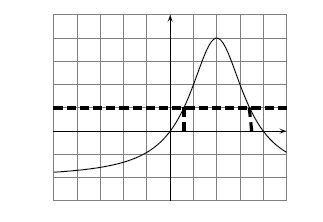
On regarde, et colorie, maintenant la partie de la courbe étant au-dessus de cette droite. Les solutions sont les abscisses de ces points.
On colorie donc la partie de l'axe des abscisses qui correspond à la partie de la courbe également coloriée.
On écrit ces solutions sous forme d'intervalle :
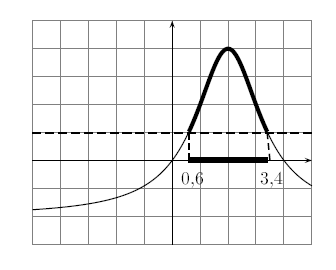
- 2) Résoudre l'inéquation .
Ici pas besoin de tracer la droite de hauteur : c'est l'axe des abscisses. Ainsi résoudre l'inéquation , c'est chercher les qui font que la courbe est au-dessous de l'axe des abscisses.
On colorie donc la partie de la courbe qui se trouve au-dessous de l'axe des abscisses, puis on colorie la partie de l'axe des abscisses qui correspond à la courbe coloriée. On trouve alors deux parties coloriées.
On écrit les solutions sous forme de réunion d'intervalles :
On fera bien attention aux bornes des intervalles : et sont exclus car on résoud une inéquation stricte : on ne veut pas que vale (on résoud , or et d'où leur exclusion).
5 - Tableau de variations
Enoncé
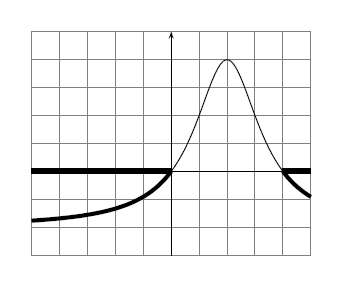
Le graphique ci-dessous représente la courbe d'une fonction sur l'intervalle .
Dresser le tableau de variations de sur l'intervalle .
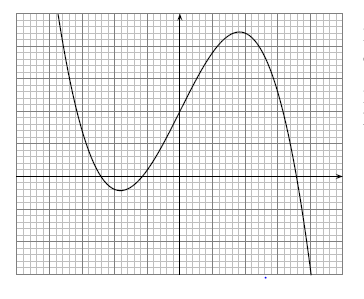
Correction
Pour dresser le tableau de variations de cette fonction, on imagine un point placé tout à gauche de la courbe et qui avance de gauche à droite (on peut aussi imaginer un ballon qui roule sur la courbe de la gauche vers la droite...). La fonction sera croissante lorsqu'on verra que le point (ou le ballon !!) "monte" et décroissante lorsqu'il "descendra".
On repère dans un premier temps une partie de la courbe qui "descend". La courbe commence à et descend jusqu'à .
La fonction sera donc décroissante sur
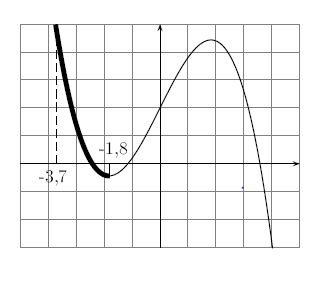
On repère ensuite une partie de la courbe qui "monte". Cette partie de la courbe commence à et monte jusqu'à .
La fonction sera donc croissante sur
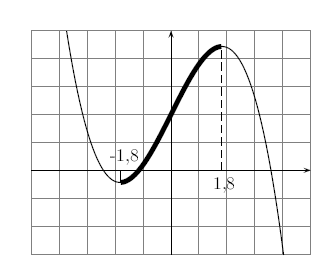
On repère, pour finir, une partie de la courbe qui "descend".
Cette partie de la courbe commence à et descend jusqu'à .
La fonction sera donc décroissante sur
On résume tout cela (on peut le faire directement) dans un tableau de variations.
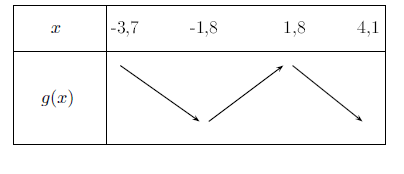
6 - Tableau de signes
Enoncé
Le graphique ci-dessous représente la courbe d'une fonction sur l'intervalle .
Dresser le tableau de signes de sur l'intervalle .
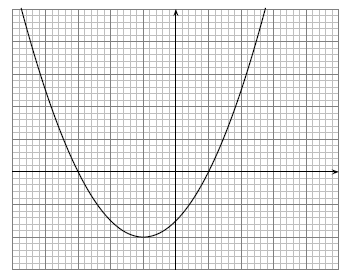
Correction
Pour connaître le signe de sur , il va falloir voir quand est-ce que la courbe est au-dessus de l'axe des abscisses (c'est-à-dire positive), et quand est-ce qu'elle est au-dessous de l'axe des abscisses (c'est-à-dire négative).
On repère dans un premier temps une partie de la courbe qui au-dessus de l'axe des abscisses.
La courbe commence à et est positive jusqu'à .
La fonction sera donc positive sur
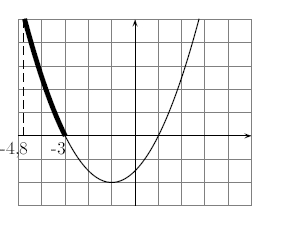
On repère ensuite une partie de la courbe qui se trouve au-dessous de l'axe des abscisses.
Cette partie de la courbe commence à et s'arrête à .
La fonction sera donc négative sur
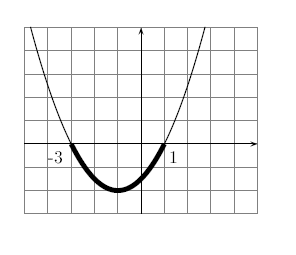
On repère, pour finir, une partie de la courbe au-dessus de l'axe des abscisses.
Cette partie de la courbe commence à et se termine en .
La fonction sera donc positive sur
On résume tout cela (on peut le faire directement) dans un tableau de variations.
On résume tout cela (on peut le faire directement) dans un tableau de signes.
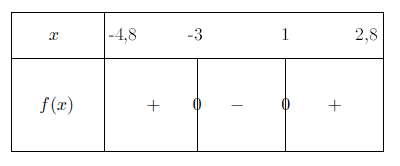
7 - Lecture du coefficient directeur d'une droite
Enoncé
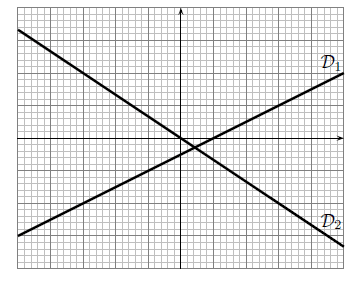
Dans le graphique ci-dessous, on a tracé deux droites représentant deux fonctions affines.
Trouver le coefficient directeur de chacune d'entre elles.
Correction
Le coefficient directeur d'une droite est donné par la formule :
, où et sont deux points de la droite.
On rappelle que si la fonction est croissante, le coefficient directeur est positif, sinon, si elle est décroissante, il est négatif.
On peut dire (de manière non formelle) que le coefficient directeur est :
combien on monte / combien on avance : pour une fonction affine croissante (droite qui "monte").
- combien on descend / combien on avance : pour une fonction affine décroissante (droite qui "descend").
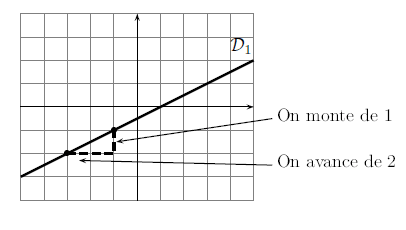
1. Coefficient directeur de
On choisit deux points bien placés sur la droite. On a pris ici les points et .
On regarde alors de combien on monte (1) pour aller du premier au second, et de combien on avance (2).
Ainsi :
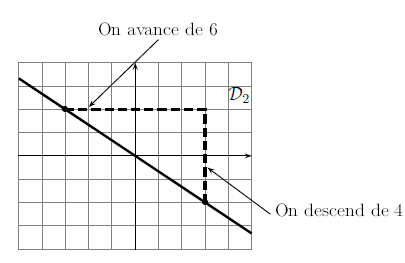
2. Coefficient directeur de
On procède ici de la même manière que pour .
On choisit deux points bien placés sur la droite. On a pris ici les points et .
On regarde alors de combien on descend (4) pour aller du premier au second, et de combien on avance (6).
Ainsi :
8- Autour de la dérivée
Dans cette partie, il faut se rappeler de l'interprétation graphique du nombre dérivé en un point.
Si on a une fonction ; un nombre , alors le nombre est le coefficient directeur de la tangente à la courbe de au point d'abscisse .
Il est donc essentiel d'avoir compris la partie précédente pour lire celle-ci.
Enoncé
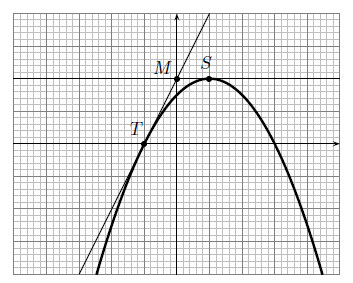
Dans le graphique ci-dessous, on a tracé la représentation graphique d'une fonction .
Les points et sont sur la courbe.
Le point est tel que les droites et sont tangentes à la courbe.
Trouver et .
Correction
- 1. Valeur de
Le nombre représente le coefficient directeur de la tangente à la courbe de au point d'abscisse . A savoir ici le coefficient directeur de .
Cette droite est horizontale, son coefficient directeur est donc nul, ainsi, .
- 1. Valeur de
Le nombre représente le coefficient directeur de la tangente à la courbe de au point d'abscisse . A savoir ici le coefficient directeur de .
Ainsi,
Toutes nos vidéos sur résolution graphique dans un repère cartésien