Suites Numériques

Pré-requis: Calculer les termes d'une suite
Connaître les suites arithmétiques, géométriques
Raisonnement par récurrence.

I. Définitions

Définition n°1 :
Une suite numérique est une fonction d’une partie de $\mathbb{N}$ dans $\mathbb{R}$

Exemples:

On peut considérer la suite $(u_{n})$ définie par : $u_{n}=n^2$
On a alors : $u_0=0$ ; $u_1=1$ ; $u_2=4$ ; $u_3=9$ ...
On considère la suite $(v_{n})$ , définie par $v_0=6$ et $\forall\in\mathbb{N}$ , $v_{n+1}=0,2v_{n}+4$
On a alors $v_1=0,2v_0+4=5,2$ , $v_2=0,2v_1+4=5,04$

Remarques:
-On dit que la suite $(u_{n})$ est définie explicitement.
On peut calculer directement des termes de « grands indices » ( $u_{100}=10000$ )

-On dit que la suite $(v_{n})$ est définie par récurrence .
Pour calculer un terme il faut connaître les termes précédents.
La suite $(v_{n})$ peut cependant être définie explicitement, pour tout entier naturel
$v_{n}=5+0,2^n$ (à montrer par récurrence)

II. Représentations graphiques

1) Suites du type $u_n=f(n)$

Méthode:
Si on veut représenter graphiquement une suite $u_n=\frac{n^2-4n+3}{5}$
on place dans le plan rapporté à un repère orthonormé les points de coordonnées $(0,u_0)$ , $(1,u_1)$ , et de manière générale « tous » les points de coordonnées $(n,u_n)$

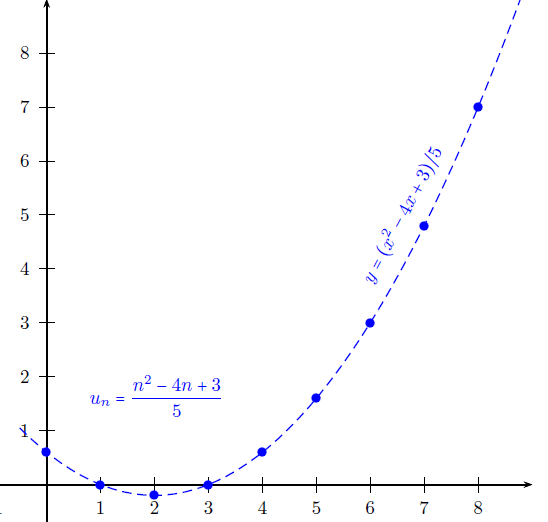
2) Suites du type $u_{n+1}=f(u_n)$

Méthode-exemple: Pour représenter graphiquement la suite $(u_n)$ , définie par:
$u_0=10$ et $u_{n+1}=\frac{u_n}{2}+\frac{2}{u_n}$
on trace sur $[0;+∞[$ la représentation graphique de la fonction $f(x)=\frac{x}{2}+\frac{2}{x}$
et la droite ∆ d’équation: $y=x$ , Les termes de la suite apparaissent alors sur l’axe des abscisses.

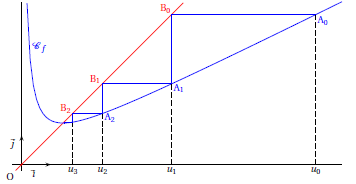
III. Comportement des suites.

1) Suites bornées.

Définition n°2 :
Soit $(u_n)$ une suite de nombre réels.
-La suite $(u_n)$ est majorée si et seulement si il existe un réel M tel que: $\forall n \in\mathbb{N}$ , $u_n \leq M$ . Un tel réel M s’appelle un majorant de la suite $(u_n)$ .

-La suite $(u_n)$ est minorée si et seulement si il existe un réel m tel que: $\forall n \in\mathbb{N}$ , $u_n \geq m$ . Un tel réel m s’appelle un minorant de la suite $(u_n)$ .

-La suite $(u_n)$ est bornée si et seulement si elle est à la fois majorée et minorée.
Ceci équivaut au fait qu’il existe deux réels m et M tels que: $\forall n \in\mathbb{N}$ , $m \leq u_n \leq M$

Exemples:
a) On considère la suite $(w_n)$ définie par pour tout entier naturel $n$ , $w_n=3+cos(n)$
On a $\forall n \in\mathbb{N}$ , $2 \leq w_n \leq 4$ (à montrer)

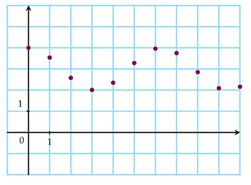
b) On considère la suite $(r_n)$ définie par $r_0=6$ et $\forall n \in\mathbb{N}$ , $r_{n+1}=\sqrt{r_n+4}$ .
On a $\forall n \in\mathbb{N}$ , $2 \leq r_n \leq 6$ (à montrer par récurrence)

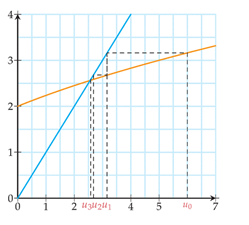
2) Sens de variation.

Définition 2. Soit $(u_n)$ une suite de nombre réels.

La suite $(u_n)$ est croissante si et seulement si pour tout entier naturel $n$ , $u_{n+1} \geq u_n$ .
La suite $(u_n)$ est décroissante si et seulement si pour tout entier naturel $n$ , $u_{n+1} \leq u_n$ .
La suite $(un)$ est constante si et seulement si pour tout entier naturel $n$ , $u_{n+1}=u_n$
La suite $(un)$ est monotone si elle est croissante ou décroissante.

:::Méthode: On étududie le signe de $u_{n+1}-u_n$
(1) Si pour tout entier n, $u_{n+1}-u_n \leq 0$ ; alors la suite $(u_n)$ est croissante.
(2) Si pour tout entier n, $u_{n+1}-u_n \geq 0$ ; alors la suite $(u_n)$ est décroissante.
:::

Remarque: Autre méthode si la suite est strictement positive, on peut comparer $\frac{u_{n+1}}{u_n}$ et $1$

Exemples:
Montrer que la suite de terme générale $u_n=\frac{3^n}{(n+1)^2}$ est strictement croissante pour tout $n \geq 1$ .

Suites Numériques

I. Définitions