Arithmétique en 3ème.

I. Rappels et vocabulaire.

1. Division euclidienne.

Exemple :
La division euclidienne de 122 par 5 est :
$122=5\times 24 + 2$
Ici,

• le dividende est 122 ;
• le diviseur est 5 ;
• le quotient est 24 ;
• le reste est 2.

2. Multiples et diviseurs.

Formellement, la division euclidienne de $a$ par $b$ s'écrit
$a=bq+r$
$r$ étant égal à 0, on obtient alors :
$a=bq$.

Exemple :

• 25 est un multiple de 5 et 5 est un diviseur de 25.
• 21 est un multiple de 7 et 7 est un diviseur de 21.

3. Critères de divisibilité.

Les critères de divisibilité sont employés pour savoir plus rapidement si un nombre $a$ est divisible par un nombre $b$, qu'avec la division euclidienne.

• Un nombre est divisible par 2 lorsque le chiffre des unités est pair. Par exemple, 2 ; 14 ; 3276 sont des nombres divisibles par 2. On les appelle aussi les nombres pairs.
• Un nombre est divisible par 5 lorsque le chiffre des unités est 0 ou 5. Par exemple, 10 ; 35 ; 2675 sont des nombres divisibles par 5.
• Un nombre est divisible par 3 lorsque la somme des chiffres qui le composent est divisible par 3. Par exemple, 3 ; 3 033 ; 981 sont divisibles par 3.
• Un nombre est divisible par 9 lorsque la somme des chiffres qui le composent est divisible par 9. Par exemple, 18 ; 3 033 ; 4 136 202 sont divisibles par 9.
• Un nombre est divisible par 4 lorsque le nombre formé des chiffres des unités et des dizaines est divisible par 4. Par exemple, 328 ; 432 ; 1 518 536 sont divisibles par 4.

Il existe d'autres critères de divisibilté, par 6, par 7, par 8, par 11, mais ils sont plus complexes et ne nous intéressent pas ici.

II. Nombres premiers

Exemple :
3 ; 7 ; 31 sont des nombres premiers : ils n'ont pas d'autres diviseurs que 1 et eux-mêmes.
6 n'est pas premier car il a 3 et 2 comme diviseurs, en plus de 1 et lui-même.

Voici la liste des 100 premiers nombres entiers naturels.

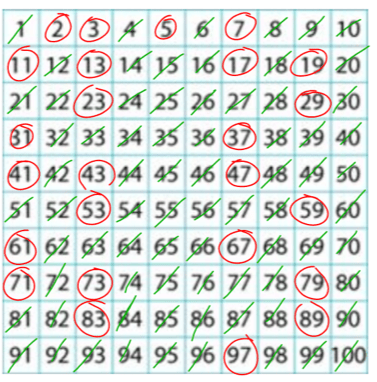
En rouge, sont entourés les nombres premiers inférieurs à 100.
On en trouve 25. On peut les déterminer en appliquant le Crible d'Eratosthène : Ce procédé consiste à entourer un nombre entier dans une liste et de barrer tous ces multiples.
Eratosthène était un mathématicien, astronome, philosophe grec de l'Antiquité. Il était à la tête de la bibliothèque d'Alexandrie et on lui doit entre autre la détermination de la circonférence de la Terre, grâce à un calcul trigonométrique.

Exemple :

• $45=5\times 9=5\times 3\times 3=3^2\times 5$
• $78=2\times 39=2\times 3\times 13$.

Remarque :
Cette dernière propriété est très importante. Elle est à la base de nombreuses théories de l'arithmétique. Elle est très utile notamment dans le cryptage de données lors de transactions financières, ce qui est à la base de notre système d'échange financier.
Le principe repose sur la difficulté de décomposer un nombre entier en produit de nombres premiers. Lorsque le nombre est très grand (composé de milliers de chiffres), cela devient quasiment impossible ! Celui qui arrivera à trouver un procédé permettant de répondre à cette problématique mettra à mal une bonne partie de notre économie...

Toutes nos vidéos sur arithmétique et nombre premiers