Homothéties et théorème de Thalès en 3ème

Ce chapitre, assez court, traite de transformations du plan. Il s'agit des homothéties. Tout comme les symétries (centrales et axiales) et les translations, les homothéties sont des transformations du plan permettant de transformer une figure géométrique.

Elles peuvent venir en introduction du théorème de Thalès, ce que nous verrons dans le deuxième paragraphe.

I. Homothéties.

Pour caractériser parfaitement une homothétie, on doit connaître le point à partir duquel on effectue la transformation, qu'on appelle centre de l'homothétie. Ainsi que le nombre par lequel on multiplie les longueurs de la figure, qu'on appelle rapport de l'homothétie.

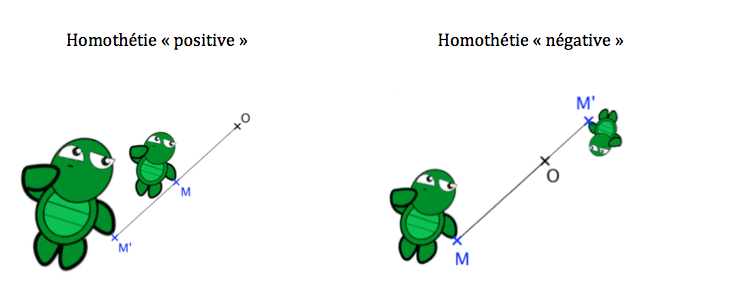
Une homothétie positive peut être comparée à un agrandissement ou une réduction.
Une homothétie négative consiste à faire une symétrie centrale avant un agrandissement ou une réduction.

Ici, les points $O$, $M$ et $M'$ sont alignés.

II. Théorème de Thalès.

1. Configuration n°1.
   
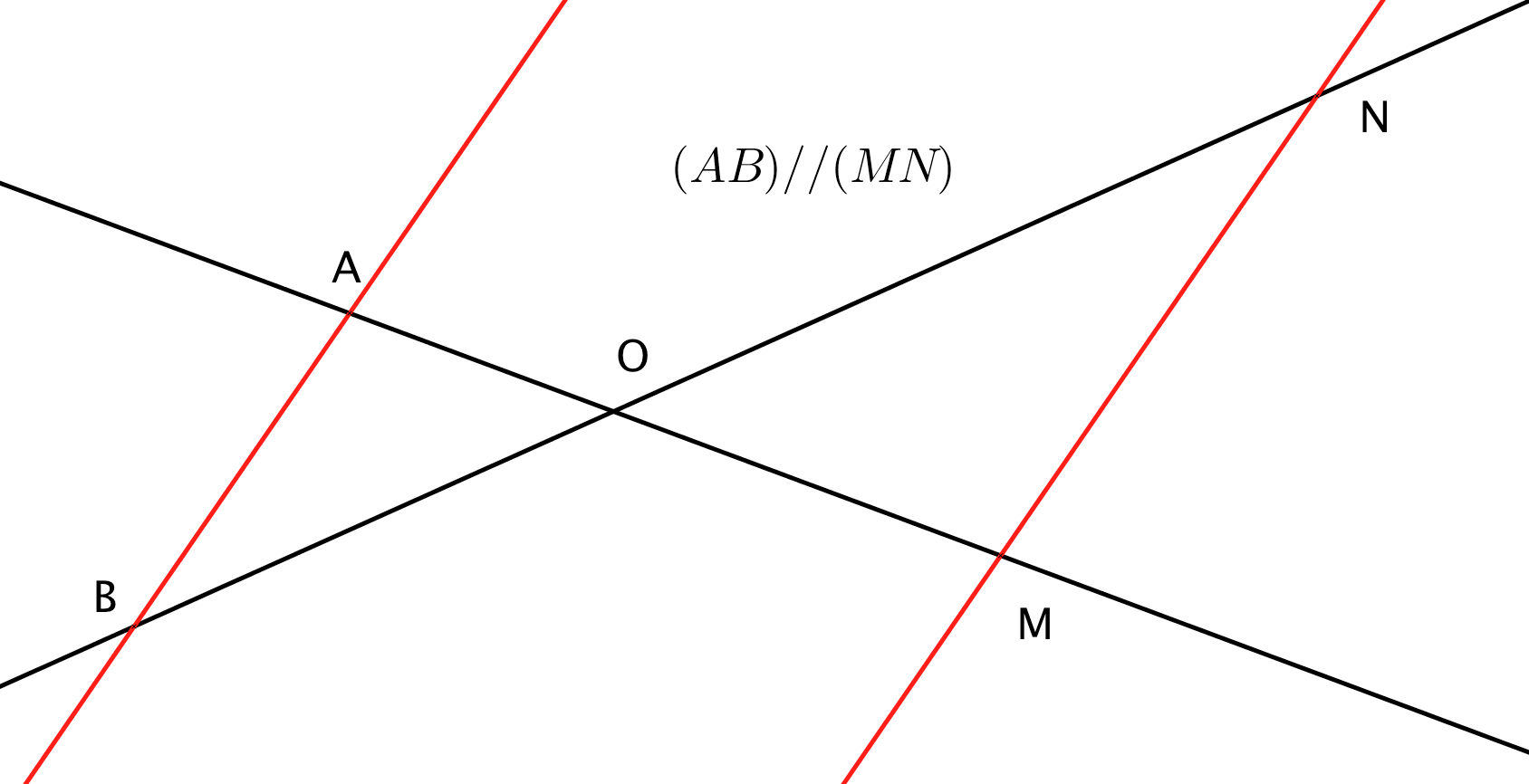
   On reconnait ici une homothétie négative de centre $O$ et de rapport :
   $\frac{AO}{OM}=\frac{BO}{ON}=\frac{AB}{MN}$

Il s'agit de la première configuration de Thalès.

2. Configuration n°2.
   
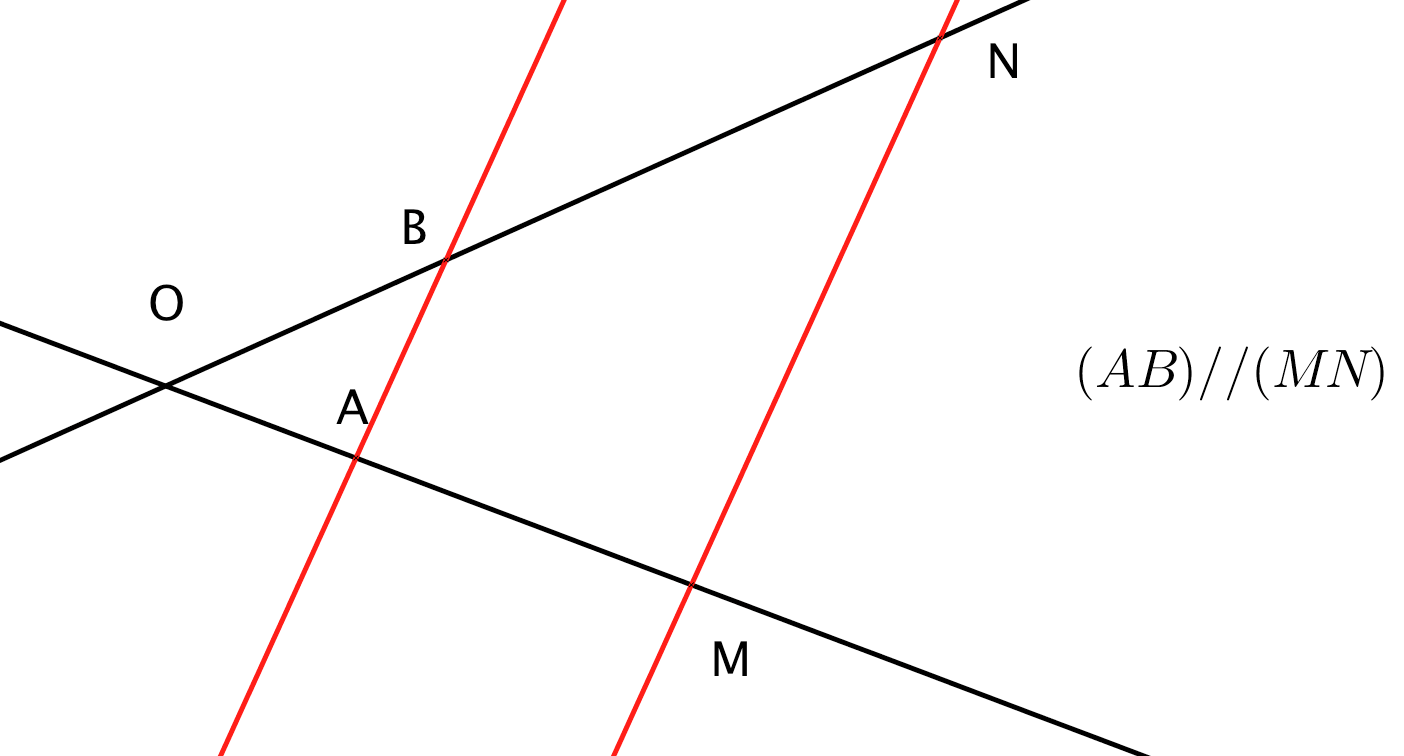
   On reconnait ici une homothétie positive de centre $O$ et de rapport :
   $\frac{MN}{AB}=\frac{MO}{AO}=\frac{NO}{BO}$

Il s'agit de la deuxième configuration de Thalès.

Remarques :
Les égalités ci-dessus portent le nom d'égalité de Thalès. On peut retrouver une autre version du théorème de Thalès, sans doute plus rigoureuse, dans le chapitre Théorème de Thalès

Toutes nos vidéos sur homothéties et théorème de thalès en 3ème