Les fonctions de références et les fonctions associées en 1ère S

I. Les fonctions de référence

1. Fonctions affines

Les fonctions affines sont définies sur $\mathbb R$ . La formule générale est donnée par :

$f(x)=ax+b$

Le nombre $a$ s'appelle le coefficient directeur et le nombre $b$ s'appelle l'ordonnée à l'origine.

En fonction de $a$ , on peut définir les variations de la fonction $f$ :
$\begin{cases}\textrm{si }a>0,\ f\textrm{ est strictement croissante} \\ \textrm{si }a<0,\ f\textrm{ est strictement décroissante} \\ \textrm{si }a=0,\ f\textrm{ est constante}\end{cases}$

La courbe représentative d'une fonction affine est une droite.

2. La fonction carrée.

La fonction carrée est définie sur $\mathbb R$ . La formule générale est donnée par :

$c(x)=x^2$

On précise les variations de la fonction carrée dans le tableau suivant :

$x$	$-\infty$	0		$+\infty$
$x^2$		0

La fonction carrée est décroissante sur $]-\infty\ ;\ 0]$ et croissante sur $[0\ ;\ \infty[$

Voici sa courbe représentative :

3. La fonction inverse.

La fonction inverse est définie sur $\mathbb R^*$ , c'est à dire pour tout $x$ différent de 0. La formule générale est donnée par :

$i(x)=\frac{1}{x}$

On précise les variations de la fonction inverse dans le tableau suivant :

$x$	$-\infty$	0		$+\infty$
$\frac{1}{x}$

La fonction inverse est décroissante sur $]-\infty\ ;\ 0[$ .
La fonction inverse est décroissante sur $]0\ ;\ +\infty[$ .

On remarque que le point $O$ est centre de symétrie de $\mathcal H$ .

4. La fonction racine carrée

Tout nombre positif ou nul admet une racine carrée, que l'on note $\sqrt x$ . Le nombre $\sqrt x$ est l'unique nombre positif vérifiant $(\sqrt x)^2=x$

La fonction racine carrée est définie sur $\mathbb R^+$ . La formule générale est donnée par :

$R(x)=\sqrt x$

Variations de la fonction racine carrée :
Soient $a$ et $b$ deux nombre positifs, tels que $0\leq a$ .
On veut comparer $\sqrt a$ et $\sqrt b$ . Pour cela, on considère leur différence :

$\sqrt a -\sqrt b=\frac{(\sqrt a-\sqrt b)(\sqrt a+\sqrt b)}{\sqrt a+\sqrt b}=\frac{a-b}{\sqrt a+\sqrt b}$

Comme $\sqrt a$ et $\sqrt b$ sont positifs, leur somme $\sqrt a+\sqrt b$ l'est aussi.
Or, nous avons supposé que $a$ . Donc $a-b<0$ , ce qui implique que

$\frac{a-b}{\sqrt a+\sqrt b}<0$

Ainsi, $\sqrt a-\sqrt b<0$ .
En conclusion,

$a$

La fonction racine carrée est donc croissante sur $\lbrack 0\ ;\ +\infty\lbrack$ .
Voici son tableau de variations :

$x$ $0$ $+\infty$

$\sqrt x$

On dit aussi que la fonction racine carrée conserve l'ordre.

Voici sa représentation graphique :

5. La fonction valeur absolue

Pour tout réel $x$ , la valeur absolue de $x$ est égale à :

$\begin{cases}x\textrm{ si }x\textrm{ est positif ;} \\ -x\textrm{ si }x\textrm{ est négatif.}\end{cases}$

On la note $\vert x\vert$

Exemple :

$\vert 3\vert=3$ ; $\vert -15\vert =-(-15)=15$

$\vert \pi -2\vert=\pi -2$ ; $\vert 3-\pi\vert =\pi -3$

Remarques :

$\vert x\vert=0 \Longleftrightarrow x=0$

$\vert x\vert=\vert -x\vert$

$\forall x\in\mathbb R,\ \sqrt x^2=\vert x\vert$

$\forall x\in\mathbb R,\ \forall y\in\mathbb R,\ \vert x \vert=\vert y\vert\Longleftrightarrow x=y\textrm{ ou }x=-y$

On pose $A(x)=\vert x\vert$ . On peut alors dire :

$\forall x\in\ ]-\infty\ ;\ 0],\ A(x)=-x$

$\forall x\in \lbrack0\ ;\ +\infty\lbrack \,\ A(x)=x$

On dit que la fonction valeur absolue est affine par morceaux.

Variations de la fonction valeur absolue :
On dresse le tableau de variations de la fonction valeur absolue.

$x$ $-\infty$ $0$ $+\infty$

$\vert x\vert$

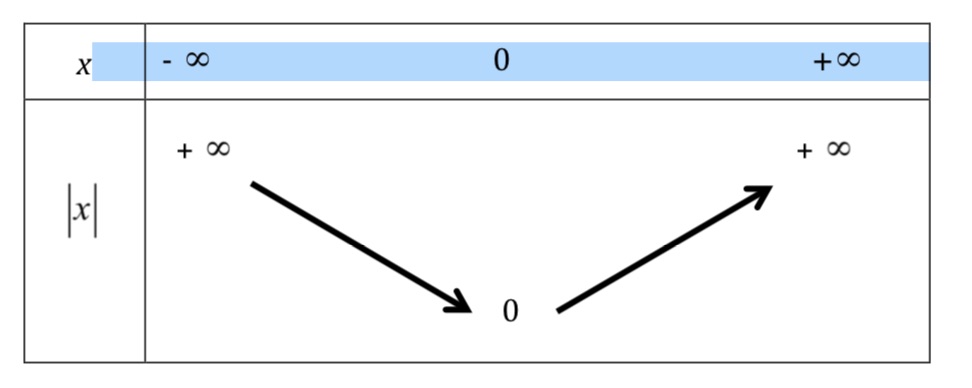
Voici sa courbre représentative :

II. Les fonctions associées.

On peut se contenter de lire les parties "Ce qu'il faut retenir", mais pour une bonne maîtrise technique, on conseille de lire attentivement les démonstrations.

Dans toute la suite, on désigne par $u$ une fonction définie sur un intervalle $I$ .

1. Variations de $u+k$ , $(k\in\mathbb R)$

Propriété :
Les fonctions $u$ et $u+k$ , avec $k\in\mathbb R$ , ont le même sens de variations.

Démonstration :
Supposons que $u$ est croissante sur $I$ .
Alors, $\forall a\in I$ , $\forall b\in I$ ,

$a$

et $\forall k\in\mathbb R$ ,

$u(a)+k$

En résumé, $a$
$u+k$ est croissante sur $I$ .
On effectue le même raisonnement lorsque $u$ est décroissante.

Ce qu'il faut retenir :
Si on ajoute un nombre à une fonction $u$ , la nouvelle fonction obtenue a les mêmes variations que $u$ .

2. Variations de $\lambda u$ , $(\lambda\neq 0)$

Propriété :

Si $\lambda >0$ , $u$ et $\lambda u$ ont les mêmes variations sur $I$ ;

Si $\lambda <0$ , $u$ et $\lambda u$ ont des variations contraires sur $I$ .

Démonstration :
Supponsons que $u$ est décroissante sur $I$ .
Alors, $\forall a\in I$ , $\forall b\in I$ ,

$au(b)$

Si $\lambda >0$ , alors

$\lambda u(a)>\lambda u(b)$

et $\lambda u$ est décroissante sur $I$ .
Si $\lambda <0$ , alors

$\lambda u(a)<\lambda u(b)$

et $\lambda u$ est croissante sur $I$ .
On effectue le même raisonnement pour $u$ décroissante.

Ce qu'il faut retenir :
Si on multiplie par un nombre une fonction $u$ , la nouvelle fonction obtenue a les mêmes variations que $u$ si le nombre est positif, et a des variations contraires si le nombre est négatif.

3. Variations de $\sqrt u$

Propriété :
$u$ est définie sur $I$ et $\forall x\in I$ , $u(x)\geq 0$
Les fonctions $u$ et $\sqrt u$ ont les mêmes variations sur $I$ .

Démonstration :
On sépare la démonstration en deux parties :

On suppose que $u$ est croissante sur $I$ .
$\forall a\in I$ , $\forall b\in I$ ,

$a$

De plus, $u(a)>0,\ u(b)>0$ et la fonction racine carrée est croissante sur $\mathbb R^+$ , donc

$u(a)$

Donc la fonction $\sqrt u$ est croissante sur $I$ .

On suppose que $u$ est décroissante sur $I$ .
$\forall a\in I$ , $\forall b\in I$ ,

$au(b)$

De plus, $u(a)>0,\ u(b)>0$ et la fonction racine carrée est croissante sur $\mathbb R^+$ , donc

$u(a)>u(b)\Longrightarrow \sqrt{u(a)}>\sqrt{u(b)}$

Donc la fonction $\sqrt u$ est décroissante sur $I$ .

4. Variations de $\frac{1}{u}$

Propriété :
$u$ est définie sur $I$ , et $\forall x\in I,\ u(x)\neq 0$ et $u(x)$ est de signe constant.
Alors les fonctions $u$ et $\frac{1}{u}$ ont des variations contraires.

Démonstations :
Supponsons que $u$ est croissante sur $I$ .

$a$

$u(a)$ et $u(b)$ ont le même signe (dans $]-\infty\ ;\ 0\lbrack$ ou $]0\ ;\ +\infty\lbrack$ )
La fonction inverse est décroissante sur $]-\infty\ ;\ 0\lbrack$ (et aussi sur $]0\ ;\ +\infty\lbrack$ )
Donc

$u(a)\frac{1}{u(b)}$

En résumé, $\frac{1}{u}$ est décroissante sur $I$ .

III. Observations des courbes

1. Positions relatives des courbes des fonctions carrée, identité et racine carrée.

La fonction $l$ définie par

$\forall x\in\mathbb R,\ l(x)=x$

est la fonction identité.

Posons, pour $x\in\lbrack 0;\ +\infty\lbrack$

$\begin{cases}l(x)=x \\ c(x)=x^2 \\ f(x)=\sqrt x\end{cases}$

et notons $\mathcal C_l,\ \mathcal C_c,\ \mathcal C_f$ leurs courbes représentatives dans un repère orthogonal $(O;\vec{i};\vec{j})$ .

Remarque :

$l(0)=c(0)=f(0)=0$

$l(1)=c(1)=f(1)=1$
Les trois courbes passent donc par le point $O$ et le point $A(1;1)$ .

$\textrm{Pour }x\in\lbrack 0; 1\rbrack,\ x^2\leq x\leq\sqrt x$

$\textrm{Pour }x\geq 1,\ \sqrt x\leq x\leq x^2$

2. Courbes de fonctions associées : exemples

Soit $f$ une fonction définie sur $I$ et $\mathcal C_f$ sa courbe représentative.

Théorème :

Soit $g$ définie sur $I$ par $g(x)=f(x)+k,\ k\in\mathbb R$
$\mathcal C_g$ est obtenue en translatant $\mathcal C_f$ d'un vecteur $k\vec{j}$ .

Soit $h$ la fonction définie sur $J$ par $h(x)=-f(x)$ . $\mathcal C_h$ est symétrique de $\mathcal C_f$ par rapport à l'axe $(xx')$ .

Exemple :
On trace les courbes représentatives des fonctions suivantes :
$f(x)=\sqrt x$ , $g(x)=\sqrt x +2$ , $h(x)=-\sqrt{x}$ .

Toutes nos vidéos sur les fonctions de référence

Les fonctions de références et les fonctions associées en 1ère S

I. Les fonctions de référence

1. Fonctions affines

2. La fonction carrée.

3. La fonction inverse.

4. La fonction racine carrée

5. La fonction valeur absolue

II. Les fonctions associées.

1. Variations de $u+k$ , $(k\in\mathbb R)$

2. Variations de $\lambda u$ , $(\lambda\neq 0)$

3. Variations de $\sqrt u$

4. Variations de $\frac{1}{u}$

III. Observations des courbes

1. Positions relatives des courbes des fonctions carrée, identité et racine carrée.

2. Courbes de fonctions associées : exemples

Toutes nos vidéos sur les fonctions de référence

Posez vos questions

Fiches méthodes

Cours de mathématiques de première S

Les fonctions de références et les fonctions associées en 1ère S

I. Les fonctions de référence

1. Fonctions affines

2. La fonction carrée.

3. La fonction inverse.

4. La fonction racine carrée

5. La fonction valeur absolue

II. Les fonctions associées.

1. Variations de u+ku+ku+k, (k∈R)(k\in\mathbb R)(k∈R)

2. Variations de λu\lambda uλu, (λ≠0)(\lambda\neq 0)(λ̸​=0)

3. Variations de u\sqrt uu​

4. Variations de 1u\frac{1}{u}u1​

III. Observations des courbes

1. Positions relatives des courbes des fonctions carrée, identité et racine carrée.

2. Courbes de fonctions associées : exemples

Toutes nos vidéos sur les fonctions de référence

Posez vos questions

Fiches méthodes

Cours de mathématiques de première S

1. Variations de $u+k$ , $(k\in\mathbb R)$

2. Variations de $\lambda u$ , $(\lambda\neq 0)$

3. Variations de $\sqrt u$

4. Variations de $\frac{1}{u}$