Modélisation et échantillonnage

I. Répétition d'expériences.

1. Expériences aléatoires.

Exemple :

1. Lancer 5 fois de suite un dé cubique bien équilibré.
2. Lancer successivement 5 dés cubiques de contenus différents.

2. Arbres pondérés.

Remarque :
Autrement dit, dans un arbre pondéré, la probabilité d'un résultat final est le produit des probabilités de >chaque branche qui y mène.

On schématise la répétition d'expériences à l'aide d'un arbre pondéré. On inscrit les probablités sur chaque branche.

Exemple n°1 :

1. On schématise les possibilités à l'aide d'un arbre. On note V une réponse vraie, F une réponse fausse.
   

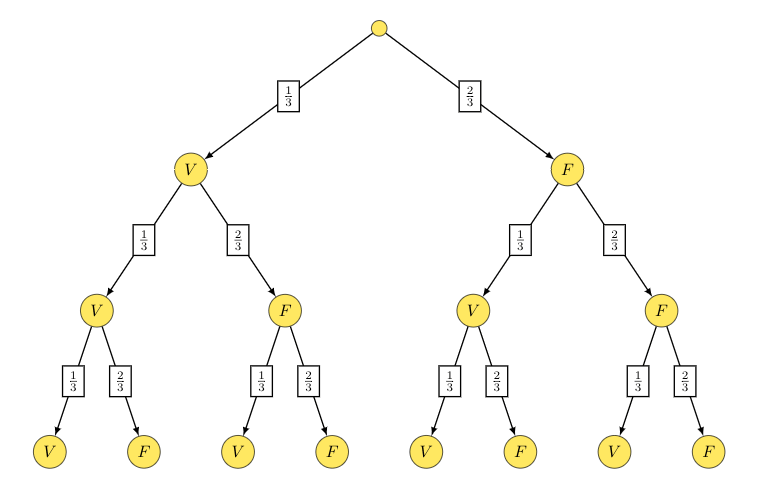
Étant donné qu'il répond au hasard, les expériences sont indépendantes.
La probabilité que la réponse soit fausse ($P(F)$) vaut toujours $\frac{2}{3}$.
La probabilité que la réponse soit vraie ($P(V)$) vaut toujours $\frac{1}{3}$.

2. Quelle est la probablité qu'il gagne 300 € ?
   Pour qu'il gagne 300 €, il doit répondre V aux trois questions :

$P(V)=\frac{1}{3}\times\frac{1}{3}\times\frac{1}{3}=\frac{1}{27}$

En répondant au hasard, il a donc 1 chance sur 27 de gagner 300 €.

3. Quelle est la probabilité de gagner 200 € ?
   Pour qu'il gagne 200 €, il doit avoir une réponse F et deux réponses V, soit VVF, VFV ou FVV.
   Il y a trois façons de placer un faux parmi trois possibilités.
   D'après l'arbre de probabilité et le principe multiplicatif, on a

$P(VVF)=\frac{1}{3}\times\frac{1}{3}\times\frac{2}{3}=\frac{2}{27}$

Ainsi,

$P(\textrm{"gagner 200"})=3\times\frac{2}{27}=\frac{6}{27}=\frac{2}{9}$

Il a donc 2 chances sur 9 de gagner 200 €.

Exemple n°2 :

On construit l'arbre pondéré correspondant à cette situation. On note aussi M s'il choisit la mer, N s'il choisit la montagne et D s'il reste à son domicile.

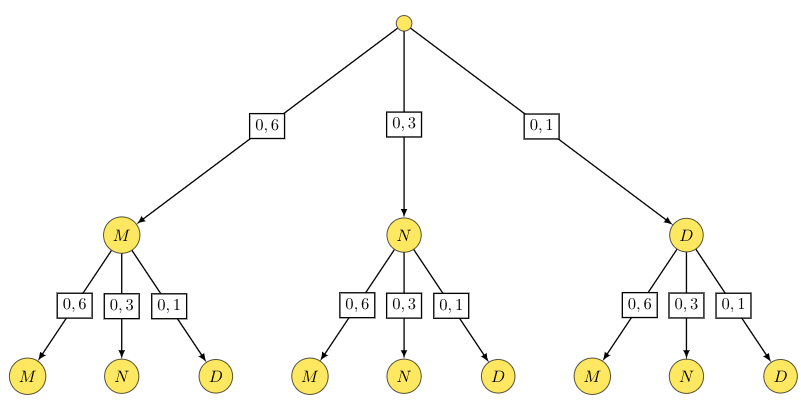
On voit sur cet arbre qu'il y a 9 issues possibles. On peut aussi retrouver ce résultat par le calcul : $3\times 3=9$ possibilités.

On s'intéresse à l'évènement suivant :

$A=\textrm{"parmi deux personnes, une au moins est allée à la mer"}$

Avec les notations prises précédemment, on a

$A=\textrm{(M et M) ou (M et N) ou (M et D) ou (N et M) ou (D et M)}$

Ainsi, on peut calculer la probablité de $A$ :

$P(A)=0{,}6\times 0{,}6 + 0{,}6\times 0{,}3 + 0{,}6\times 0{,}1+0{,}3\times 0{,}6+0{,}1\times 0{,}6=0{,}84$

La probabilité que, parmi deux personnes, une au moins soit allée à la mer est de 0,84, soit 84 %.

• Les trois personnes ont été à la mer : $0{,}6^3=0{,}216$
• Deux ont été à la mer : les évènements sont $MM\overline{M}$ ou $M\overline{M} M$ ou $\overline{M} MM$. Donc la probabilité est de : $3\times 0{,}6\times 0{,}6\times 0{,}4=0{,}432$
• Un seul a été à la mer : les évènements sont $M\overline{M}\ \overline{M}$ ou $\overline{M} M\overline{M}$ ou $\overline{M}\ \overline{M} M$. Donc la probabilité est de : $3\times 0{,}6\times 0{,}4\times 0{,}4=0{,}288$

Remarque :

• Si vous vous demandez d'où vient ce "0,4" dans les calculs, il faut remarquer que l'évènement $\overline{M}$ est l'évènement contraire de l'évènement $M$, soit $N$ ou $D$. On additionne les probabilités de $N$ et $D$, soit $0{,}3 + 0{,}1=0{,}4$.
• Sur l'arbre précédent, il n'y est pas indiqué lorsqu'on s'intéresse à trois personnes. Il faut rajouter trois branches au bout de chacune des neuf branches existantes, avec les mêmes probabilités.

Toutes nos vidéos sur modélisation et échantillonnage en 1ère s