Trigonométrie en 1ère S.

I. Le cercle trigonométrique.

1. Rappels et notations.

On note $\mathcal C$ le cercle trigonométrique, c'est-à-dire un cercle de centre $O$ et de rayon 1, d'origine $O$ et orienté positivement.
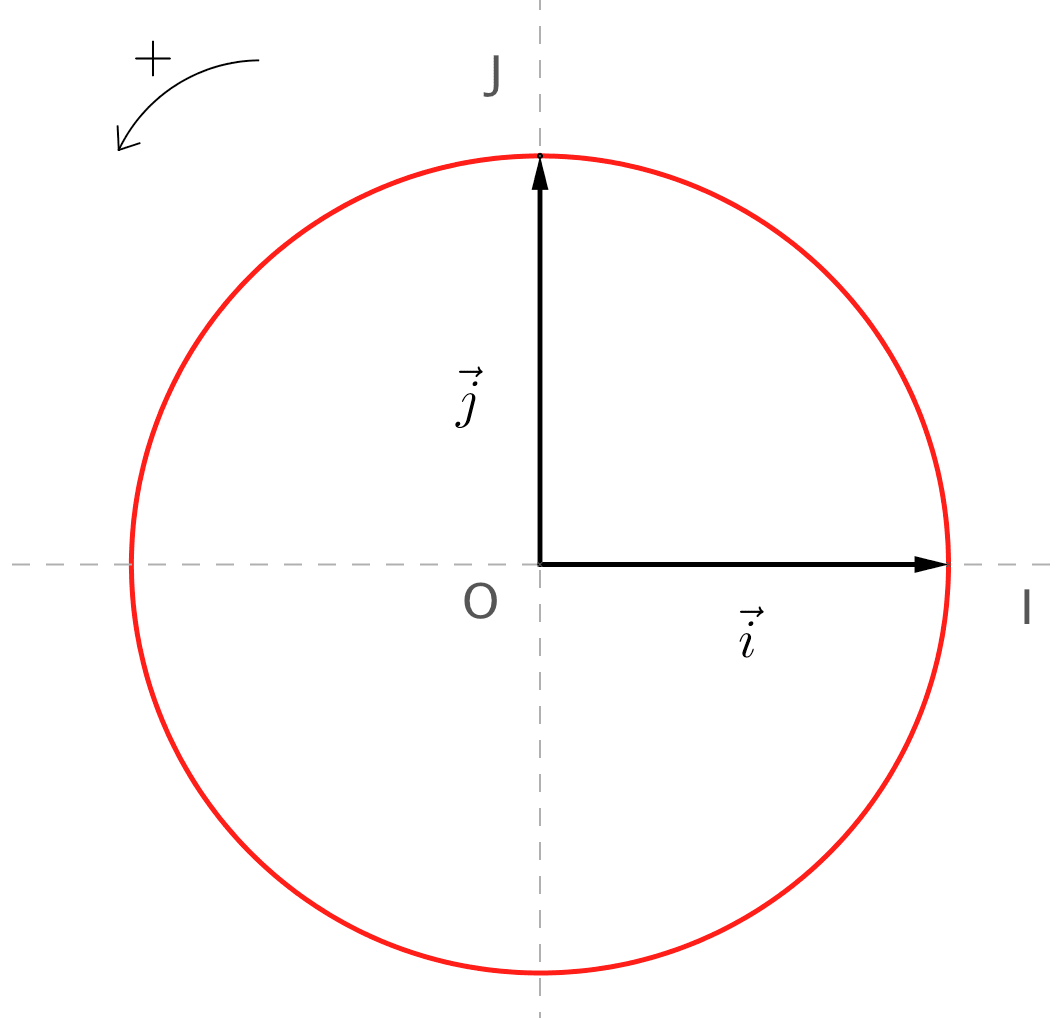
cercle-trigonometrique
Grâce à l'algorithme d'enroulement de la tangente $\mathcal (D)$ au cercle trigonométrique rappelé ci-dessous, on peut associer à tout réel $x$ un unique point $M(x)$ du cercle $\mathcal C$ .
On remarque alors que :
" $x$ repère le point" ou " $x$ est une mesure de l'angle $\widehat{IOM}$ "

Propriété :
Pour tout réel $x$ et tout entier $k$ , les points $M(x)$ et $M(x+2k\pi)$ sont confondus.

Remarque :
Le sens positif, ou trigonométique correspond au sens contraire des aiguilles d'une montre.

2. Mesure en radian d'un angle.

Définition :
Soit $N$ le point de $\mathcal (D)$ d'abscisse 1 et $M$ le point de $\mathcal C$ associé au réel 1 (en enroulant $\mathcal (D)$ autour de $\mathcal C$ ).
On définit 1 radian comme la mesure de l'angle $\widehat{IOM}$ ainsi construit.
On note aussi 1 rad.

Remarque :
La mesure en radian d'un angle $\widehat{IOM}$ correspond à la longueur de son arc $IM$ .

Propriété :
Les mesures en degrés et en radians d'un angle géométrique sont proportionnelles.

La méthode de conversion repose sur le tableau de proportionnalité suivant :

Mesure en degrés	180	$d$
Mesure en radians	$\pi$	$\alpha$

On peut résumer les différentes correspondances usuelles dans le tableau suivant :

$x$ en radians	0	$\frac{\pi}{6}$	$\frac{\pi}{4}$	$\frac{\pi}{3}$	$\frac{\pi}{2}$	$\frac{2\pi}{3}$	$\frac{3\pi}{4}$	$\frac{5\pi}{6}$	$\pi$	$2\pi$
$x$ en degrés	0	30	45	60	90	120	135	150	180	360

3. Mesure principale d'un angle.

Un angle possède en radians un infinité de mesures :
Si $\alpha$ en est une, alors $\alpha -4\pi$ , $\alpha -2\pi$ , $\alpha +2\pi$ ... en sont d'autres...
Le périmètre du cercle trigonométrique étant de mesure $2\pi$ , on a la définition suivante :

La mesure principale d'un angle est sa mesure en radians dans l'intervalle $]-\pi\ ;\ \pi ]$ .

II. Angles de vecteurs.

Dans toute cette partie, $\vec u$ et $\vec v$ sont deux vecteurs non nuls.

1. Définitions et mesure d'un angle de vecteurs.

Le couple $(\vec u\ ;\ \vec v)$ est appelé angle orienté de vecteurs.

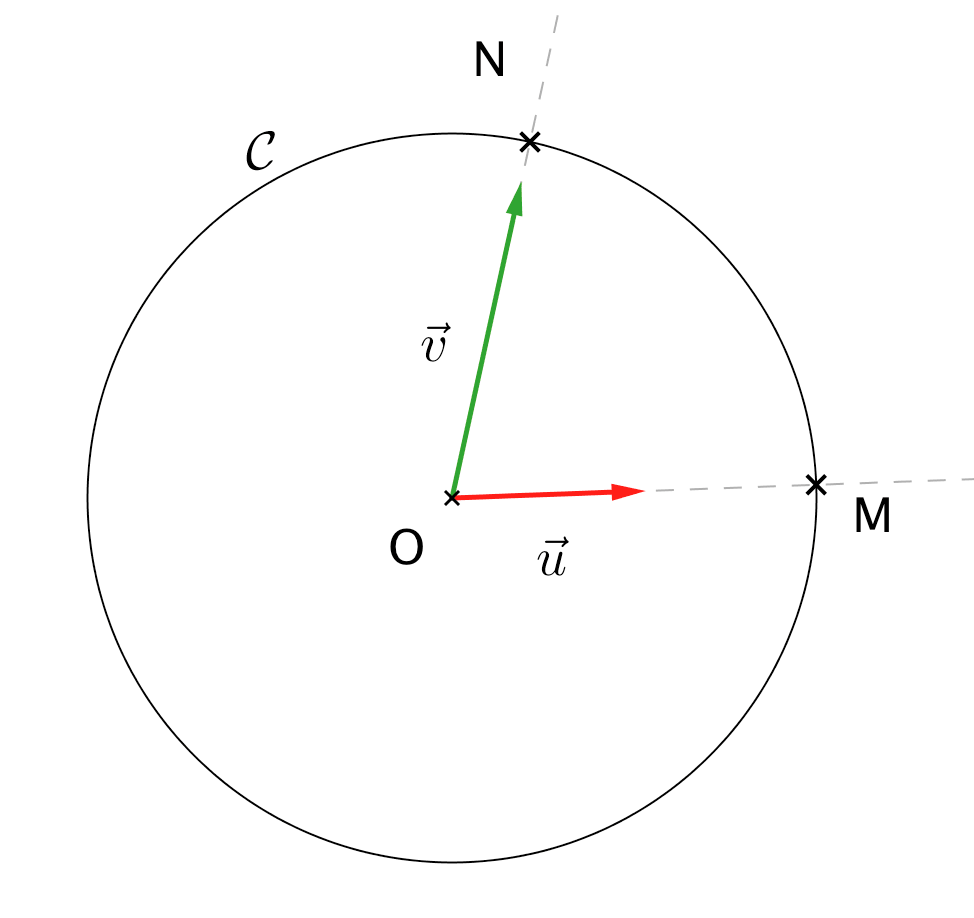
angle de vecteurs

Sur la figure ci-dessus, les vecteurs $\vec u$ et $\vec v$ dirigent les demi-droites d'origine $O$ et passant par $M$ et $N$ respectivement.
Ainsi, une mesure de l'angle $(\vec u\ ;\ \vec v)$ est aussi une mesure de l'angle $(\overrightarrow{OM}\ ;\ \overrightarrow{ON})$ .

Définition :
Soit $M(x)$ et $N(y)$ deux points du cercle trigonométrique.
On appelle mesure de l'angle orienté $(\overrightarrow{OM}\ ;\ \overrightarrow{ON})$ le réel $y-x$ .

Notations :
Si $\alpha$ est une mesure de l'angle orienté $(\vec u\ ;\ \vec v)$ , alors pour tout entier $k$ , le réel $\alpha\ +2k\pi$ est une mesure de l'angle $(\vec u\ ;\ \vec v)$ .
On dit alors que l'angle orienté $(\vec u\ ;\ \vec v)$ a pour mesure $\alpha$ modulo $2\pi$
On écrit aussi :
$(\vec u\ ;\ \vec v)=\alpha[2\pi]$

Remarques :
On dit qu'une mesure d'angle est définie à $2\pi$ près : deux mesures d'angles d'un même angle orienté sont distantes d'au moins $2\pi$ .

Conséquences :

Les mesures des angles $(\vec u\ ;\ \vec v)$ et $(\vec v\ ;\ \vec u)$ sont opposées:
$(\vec v\ ;\ \vec u)=-(\vec u\ ;\ \vec v)\ [2\pi]$ ;

$(\vec u\ ;\ \vec u)=0[2\pi]$ (angle nul) ;

$(\vec u\ ;\ -\vec u)=\pi [2\pi]$ (angle plat) ;

Si $(\vec u$ et $\vec v)$ sont orthogonaux et non nuls, alors $(\vec u\ ;\ \vec v)=\frac{\pi}{2}[\pi]$ (angles droit) ;

La mesure de l'angle orienté $(\vec u\ ;\ \vec v)$ dans l'intervalle $]-\pi\ ;\ \pi ]$ est sa mesure principale.

2. Propriétés des angles orientés.

Propriétés :
$k$ et $k'$ sont deux réels ; $\vec u$ , $\vec v$ et $\vec w$ sont trois vecteurs non nuls.

$(\vec u\ ;\ \vec v)=(\vec u\ ;\ \vec w)+(\vec w\ ;\ \vec v)[2\pi]$ ;
Si $k$ et $k'$ sont de mêmes signes, alors $(k\vec u\ ;\ k'\vec v)=(\vec u\ ;\ \vec v)[2\pi]$ ;
Si $k$ et $k'$ sont de signes contraires, alors $(k\vec u\ ;\ k'\vec v)=\pi + (\vec u\ ;\ \vec v)[2\pi]$ ;
$(\vec u\ ;\ \vec v)=0[\pi]$ si et seulement si les vecteurs $\vec u$ et $\vec v$ sont colinéaires.

III. Cosinus et sinus

1. Définitions et premières propriétés

Définition :
Un repère orthonormé $(O\ ;\ \vec i\ ,\ \vec j)$ est dit

direct si $(\vec i\ ;\ \vec j)=+\frac{\pi}{2}$ ;
indirect si $(\vec i\ ;\ \vec j)=-\frac{\pi}{2}$ .

Définition :
Soit $x$ un réel et $M$ son point associé sur le cercle trigonométrique.

Le cosinus de $x$ est l'abscisse du point $M$ dans le repère $(O\ ;\ \vec i\ ,\ \vec j)$ ; il est noté $\cos (x)$
Le sinus de $x$ est l'ordonnée du point $M$ dans le repère $(O\ ;\ \vec i\ ,\ \vec j)$ ; il est noté $\sin (x)$

Remarque :
Dans le repère $(O\ ;\ \vec i\ ,\ \vec j)$ , le point $M$ associé au réel $x$ a pour coordonnées $(\cos (x)\ ;\ \sin (x))$ .

Propriétés immédiates :
Pour tout réel $x$ ,

$\cos^2 (x) + \sin^2 (x)=1$ ;
$-1\leq\cos (x)\leq 1$ et $-1\leq\sin (x)\leq 1$ ;
$\cos (x+2k\pi)=\cos (x)$ et $\sin (x+2k\pi)=\sin (x)$ pour $k\in\mathbb Z$ .

2. Propriétés des angles associés.

On considère $x$ un réel donné et $M$ le point associé sur le cercle trigonométrique $\mathcal C$ .
Grâce aux propriétés de symétrie du cercle, certains autres points du cercle ont des coordonnées pouvant se déduire de celles de $M(\cos (x)\ ;\ \sin (x))$ .
Ces points permettent de définir ce que l'on appelle des angles associés.

Propriétés des angles associés :

$\cos(-x)=\cos (x)$
$\sin(-x)=-\sin (x)$

Propriétés des angles supplémentaires :

$\cos (\pi -x)=-\cos (x)$ et $\cos (\pi +x)=-\cos (x)$
$\sin (\pi -x)=\sin (x)$ et $\sin (\pi +x)=-\sin (x)$

Propriétés des angles complémentaires :

$\cos (\frac{\pi}{2} -x)=\sin (x)$ et $\cos (\frac{\pi}{2} +x)=-\sin (x)$
$\sin (\frac{\pi}{2} -x)=\cos (x)$ et $\sin (\frac{\pi}{2} +x)=\cos (x)$

Remarque :
Toutes ces propriétés peuvent se retrouver facilement sur le cercle trigonométrique suivant, en se rappelant que le cosinus d'un réel se lit sur l'axe des abscisses, alors que le sinus d'un réel se lit sur l'axe des ordonnées.
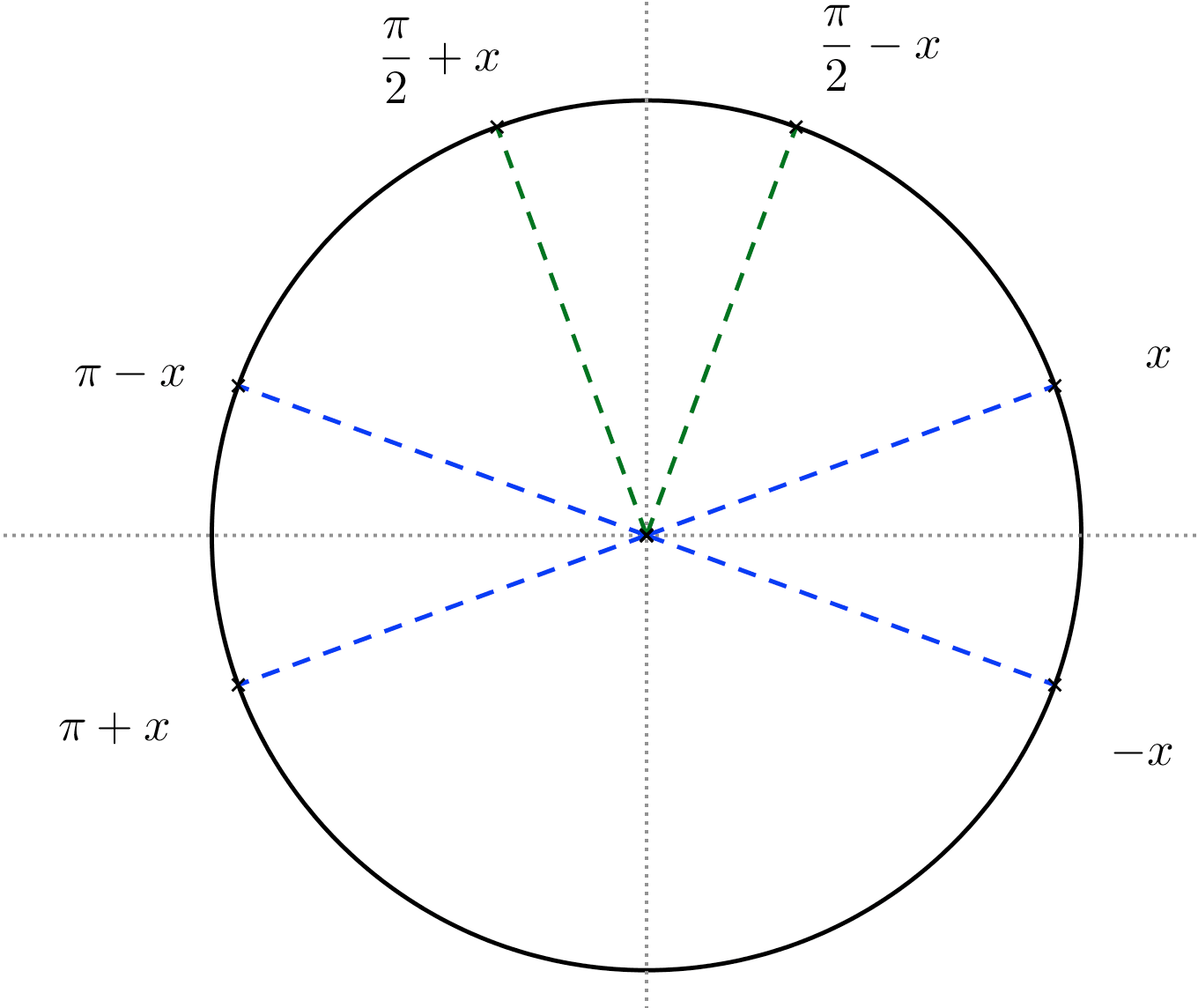
cercle trigo et cosinus

En cliquant sur cette fiche complète des formulaires de trigonométrie , vous aurez accès à un résumé très utile et très important qui regroupe de nombreuses propriétés liant cosinus et sinus.