Statistiques en 1ère S
I. Quelques définitions
Voici une liste des différentes définitions qui seront nécessaires pour maîtriser les statistiques en 1ère S.
- Une série statistique peut être donnée par un tableau du type :
| caractères | ||||||
|---|---|---|---|---|---|---|
| effectifs de chaque caractère |
On appelle fréquence du caractère : où
- On appelle étendue de la série statistique le réel
- La moyenne d'une série statistique est le nombre
Remarque : lorsque le caractère est donné sous la forme d'intervalle (ex : \[10;20\[), on convient de poser , le centre de l'intervalle.
- La médiane de la série est la valeur du caractère qui partage les valeurs de la série en deux parties de même effectif.
- Le premier quartile d'une série statistique est la plus petite valeur telle qu'au moins 25% des valeurs de la série lui sont inférieures ou égales. On le note .
- Le troisième quartile d'une série statistique est la plus petite valeur telle qu'au moins 75% des valeurs de la série lui sont inférieures ou égales. On le note .
- L'intervalle s'appelle l'intervalle interquartile
- Le nombre s'appelle l'écart interquartile.
- Le premier décile d'une série statistique est la plus petite valeur telle qu'au moins 10% des valeurs de la série lui sont inférieures ou égales. On le note .
- Le neuvième décile d'une série statistique est la plus petite valeur telle qu'au moins 75% des valeurs de la série lui sont inférieures ou égales. On le note .
On représente alors la série statistique à l'aide d'un diagramme en boite :
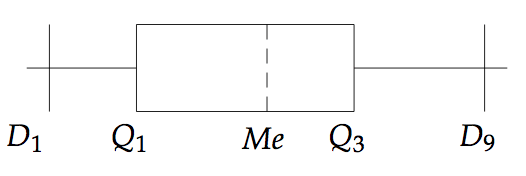
II. Dispersion d'une série statistique.
Défintion :
- La variance d'une série statistique est le nombre défini par :
- L'écart-type est noté et défini par : .
Remarques :
- La variance est un nombre positif.
- On peut aussi écrire :
- La plupart du temps, on utilise les fonctionnalités de la calculatrice poue déterminer l'écart-type d'une série.
Toutes nos vidéos sur statistiques en 1ère s