Du nombre dérivé à la fonction dérivée

Objectifs

J'ai voulu dans ce cours rappeler quelques fondements théoriques sur la dérivation, notamment sur l'interprétation graphique du nombre dérivé, illustrée par une vidéo.

Les lycéens manipulent les fonctions dérivées à tour de bras à partir de la première, mais ont souvent oublié leur signification. La question de la lecture graphique du nombre dérivé tombe pourtant régulièrement au bac et les élèves ont bien intérêt à s'en souvenir.

Une vidéo illustre la signification graphique du nombre dérivé de $f$ en $a$, $f'(a)$, à savoir le coefficient directeur de la tangente à la courbe représentative de $f$ au point d'abscisse $a$.

Si l'on a bien compris le concept de fonction, la fin de l'article veut lier le concept de nombre dérivé à celui de fonction dérivée.

Définition du nombre dérivé

Bien que la notion de « limite » ne soit plus définie dans le programme de 1ère , le nombre dérivé d’une fonction $f$ en $a$, noté $f'(a)$ est le résultat du calcul d’une limite :

$f'(a)=\lim\limits_{h \rightarrow 0} \dfrac{f(a+h)-f(a)}{h}$

Avant de poursuivre, nous allons d’abord digérer cette formule très abstraite avec une vidéo donnant l’interprétation graphique de ce calcul !

Interprétation graphique du nombre dérivé

Résumé cours vidéo

Comme expliqué dans la vidéo, le nombre dérivé de $f$ en $a$, noté $f'(a)$ est le coefficient directeur à la tangente à $Cf$ au point d’abscisse $a$. ($Cf$ désignant la courbe représentative de la fonction $f$).

Illustration

Sur l’image ci-dessous, la courbe $Cf$ est tracée en vert, la tangente au point d’abscisse $a$ en rouge, son coefficient directeur est donc $f'(a)$ :

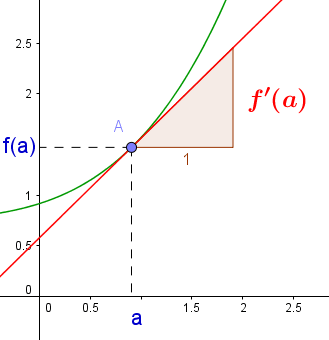
Exemple simple du calcul d’un nombre dérivé

Prenons la fonction $f$ définie par $f(x)=x^2$

Voici les quelque lignes de calcul permettant d’obtenir le nombre dérivé de $f$ en $a$ :

$\lim\limits_{h \rightarrow 0} \dfrac{f(a+h)-f(a)}{h} = f'(a)=\lim\limits_{h \rightarrow 0} \dfrac{(a+h)^2-a^2}{h}$

$=\lim\limits_{h \rightarrow 0} \dfrac{(a+h+a)(a+h-a)}{h}$

$=\lim\limits_{h \rightarrow 0} \dfrac{(2a+h)h}{h}$

$=\lim\limits_{h \rightarrow 0} (2a+h)$

$=2a$

$= f'(a)$

Gloups !
Devra-t-on à chaque fois qu’on a affaire à la fonction carré refaire ce calcul ?

Du nombre dérivé à la fonction dérivée

Non on ne refera le même calcul à chaque fois ! On retiendra par cœur que pour la fonction carré, $f'(a)=2a$ ou encore que lorsque $f(x)=x^2$ alors $f'(x)=2x$.

Ce processus automatique qui permet d’associer un nombre $x$ à un nombre dérivé $f'(x)$ s’appelle la fonction dérivée.

Ainsi la fonction dérivée de la fonction carré est $2x$. Et la fonction dérivée d’une fonction affine du type $mx+p$ est $m$, etc.

Liste non exhaustive des fonctions dérivées

Ci-dessous une liste non exhaustive des fonctions dérivées, au programme de 1ère.

• $x$ est la variable.
• $m$, $p$ et $k$ sont des constantes réelles.
• $n$ est un nombre entier non nul.
• $u$ et $v$ sont des fonctions.

Remarques :

• La vidéo et le cours sont accessibles en suivant le lien : https://cours-thierry.paris/nombre-derive-a-fonction-derivee/.

• Post Scriptum : si vous souhaitez utiliser le fichier de la fonction dérivée utilisée dans ce cours, cliquez sur le lien suivant : https://ggbm.at/bgH7VEKZ

Par Thierry

Toutes nos vidéos sur nombre dérivé et fonction dérivée